Stokes sayısı

Stokes sayısının farklı etkilerini gösteren bir illüstrasyon. Turuncu ve yeşil yörüngeler, sırasıyla küçük ve büyük Stokes sayıları için verilmiştir. Turuncu eğri, birden küçük Stokes sayısına sahip ve akış çizgilerini (mavi) takip eden bir parçacığın yörüngesini, yeşil eğri ise birden büyük Stokes sayısına sahip ve akış çizgilerini takip etmeyen bir parçacığın yörüngesini göstermektedir. Bu parçacık, sarı renkle gösterilen noktada engellerden birine (kahverengi daireler) çarpmaktadır.

Stokes sayısı (Stk), George Gabriel Stokes'un adını taşıyan ve parçacıkların bir akışkan akışı içerisinde süspansiyonda gösterdiği davranışı karakterize eden bir boyutsuz sayıdır. Stokes sayısı, bir parçacığın (veya damlanın) karakteristik zamanı ile akışın veya bir engelin karakteristik zamanı arasındaki oran olarak şu şekilde tanımlanır:

$\mathrm {Stk} ={\frac {t_{0}\,u_{0}}{l_{0}}}$

Burada, $t_{0}$ parçacığın relaksasyon süresi (İng. relaxation time; sürüklenme nedeniyle parçacık hızının üstel olarak azaldığı zaman sabiti), $u_{0}$ engelden uzakta akışın akışkan sürati ve $l_{0}$ engelin karakteristik boyutu (genellikle çapı) veya akıştaki karakteristik bir uzunluk ölçeğidir (örneğin sınır tabakası kalınlığı). Düşük Stokes sayısına sahip bir parçacık akış çizgilerini takip eder (mükemmel adveksiyon), oysa büyük Stokes sayısına sahip bir parçacık ataletinin etkisi altındadır ve başlangıç yörüngesini izlemeye devam eder.

Stokes akışı durumunda, yani parçacık (veya damlacık) Reynolds sayısı yaklaşık olarak birden küçük olduğunda, parçacığın sürükleme katsayısı Reynolds sayısının kendisiyle ters orantılıdır. Bu durumda, parçacığın karakteristik zamanı şu şekilde ifade edilebilir:

$t_{0}={\frac {\rho _{p}d_{p}^{2}}{18\mu _{g}}}$

Burada, $\rho _{p}$ parçacığın yoğunluğu, $d_{p}$ parçacık çapı ve $\mu _{g}$ akışkanın dinamik viskozitesidir.

Deneysel akışkan dinamiğinde, Stokes sayısı, parçacık görüntü velocimetrisi (PIV) deneylerinde, çok küçük parçacıkların türbülanslı akışlara katılması ve akışkan hareketinin hızını ve yönünü (aynı zamanda akışkanın hız alanı olarak da bilinir) belirlemek amacıyla optik olarak gözlemlenmesi durumunda bir akış izleyici doğruluğu ölçütüdür. Kabul edilebilir izleme doğruluğu için, parçacık yanıt süresi, akışın en küçük zaman ölçeğinden daha hızlı olmalıdır. Küçük Stokes sayıları daha iyi izleme doğruluğunu gösterir; $\mathrm {Stk} \gg 1$ durumunda, parçacıklar özellikle akışın ani bir şekilde yavaşladığı yerlerde akıştan ayrılacaktır. $\mathrm {Stk} \ll 1$ durumunda, parçacıklar akış çizgilerini yakından takip eder. Eğer $\mathrm {Stk} <0.1$ ise, izleme doğruluğu hataları yüzde 1'in altında kalır.

Parçacık görüntü velocimetrisinde (PIV) relaksasyon süresi ve izleme hatası

PIV için izleme doğruluğu açısından iki farklı parçacık boyutunun karşılaştırılması. Propilen glikolün simüle edilmiş parçacıkları (mavi noktalar) durgunluk noktası akış alanında (gri akış çizgileri) taşınmaktadır. 1 mm parçacıkların durgunluk plakasına çarptığına, 0.1 mm parçacıkların ise akış çizgilerini takip ettiğine dikkat edin.

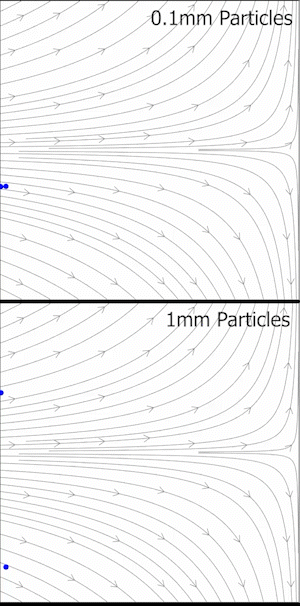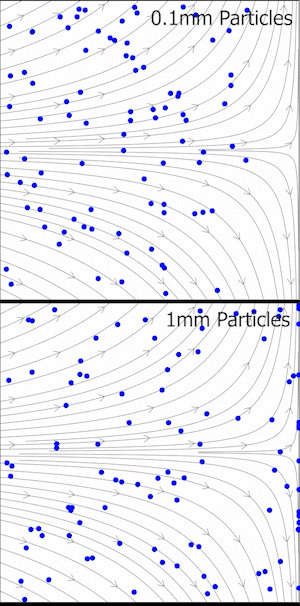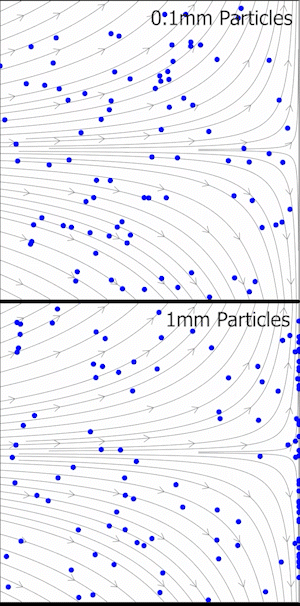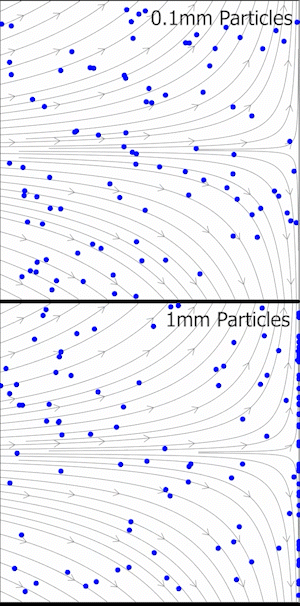
Stokes sayısı, daha önce tartışıldığı gibi, PIV veri setlerinin kalitesini değerlendirmek için bir ölçüt sunar. Ancak, her uygulamada karakteristik bir hız veya uzunluk ölçeğinin tanımı açık olmayabilir. Bu yüzden, izleme gecikmesinin nasıl ortaya çıktığını daha iyi anlamak için, Stokes rejimindeki bir parçacığın diferansiyel denklemlerinin tanımlanması gereklidir. Belirli bir hızla $v_{p}(t)$ hareket eden bir parçacık, akışkanın değişken hız alanıyla karşılaşacaktır. Parçacığın Lagrangian referans çerçevesinde akışkanın hızının $v_{f}(t)$ olduğunu varsayalım. Bu hızlar arasındaki fark, parçacığın yolunu düzeltmek için gerekli sürükleme kuvvetini oluşturur:

$\Delta v(t)=v_{f}(t)-v_{p}(t)$

Stokes sürükleme kuvveti şu şekilde tanımlanır:

$F_{D}=3\pi \mu d_{p}\Delta v$

Parçacığın kütlesi ise şu şekilde hesaplanır:

$m_{p}=\rho _{p}{\frac {4}{3}}\pi {\bigg (}{\frac {d_{p}}{2}}{\bigg )}^{3}=\rho _{p}{\frac {\pi d_{p}^{3}}{6}}$

Bu bağlamda, Newton'un ikinci yasasına göre parçacığın ivmesi şu şekilde bulunabilir:

${\frac {dv_{p}(t)}{dt}}={\frac {F_{D}}{m_{p}}}={\frac {18\mu }{{d_{p}}^{2}\rho _{p}}}\Delta v(t)$

Relaksasyon süresi olan $t_{0}={\frac {\rho _{p}d_{p}^{2}}{18\mu _{g}}}$ yerine konularak, ifade şu hale getirilir:

${\frac {dv_{p}(t)}{dt}}={\frac {1}{t_{0}}}\Delta v(t)$

Yukarıdaki birinci derece diferansiyel denklem, Laplace dönüşümü yöntemi ile şu şekilde çözülebilir:

$t_{0}sv_{p}(s)=v_{f}-v_{p}(s)$

${\frac {v_{p}(s)}{v_{f}(s)}}={\frac {1}{t_{0}s+1}}$

Bu çözüm, frekans alanında, karakteristik zamanı $t_{0}$ olan birinci dereceden bir sistemi tanımlar. Bu nedenle, −3 dB kazanç (kesim) frekansı şu şekilde olacaktır:

$f_{-3{\text{ dB}}}={\frac {1}{2\pi t_{0}}}$

Kesim frekansı ve parçacık transfer fonksiyonu, yan panelde çizilen grafikte, dengesiz akış uygulamalarında PIV hatasının ve bu hatanın türbülans spektral nicelikleri ve kinetik enerji üzerindeki etkisinin değerlendirilmesini sağlar.

Havada farklı parçacık çapları için propilen glikol parçacığının Bode grafiği.

Şok dalgası üzerinden geçen parçacıklar

Önceki bölümde tartışılan parçacık izleme yanılma hatası, frekans alanında belirgindir, ancak parçacık hareketinin akış alanı ölçümleri yapmak amacıyla izlendiği durumlarda (örneğin, parçacık görüntü velocimetrisinde) bunu değerlendirmek zor olabilir. Yukarıda belirtilen diferansiyel denklemin basit fakat anlamlı bir çözümü, zorlama fonksiyonu $v_{f}(t)=V_{u}-\Delta VH(t)$ bir Heaviside basamak fonksiyonu olduğunda mümkündür; bu, bir şok dalgası üzerinden geçen parçacıkları temsil eder. Bu durumda, $V_{u}$ şokun yukarısındaki akış hızıdır; $\Delta V$ ise şok boyunca meydana gelen hız düşüşüdür.

Bir parçacığın basamak yanıtı basit bir üstel fonksiyondur:

$v_{p}(t)=(V_{u}-\Delta V)+\Delta Ve^{-t/t_{0}}$

Hızı zamanın bir fonksiyonu olarak, parçacık hız dağılımını mesafenin bir fonksiyonu olarak dönüştürmek amacıyla, $x$ yönünde 1 boyutlu bir hız sıçraması olduğunu varsayalım. Şok dalgasının $x=0$ konumunda olduğunu varsayalım ve ardından önceki denklemi entegre edelim:

$x_{\text{particle}}=\int _{0}^{\Delta t}v_{p}(t)dt=\int _{0}^{\Delta t}(V_{u}-\Delta V)dt+\int _{0}^{\Delta t}\Delta Ve^{-t/t_{0}}dt$

$x_{\text{particle}}=\Delta t(V_{u}-\Delta V)+\Delta t\Delta V(1-e^{-\Delta t/t_{0}})$

$\Delta t=3t_{0}$ (hızın \% 95 değişim süresi) relaksasyon süresini dikkate alarak, şu sonucu elde ederiz:

$x_{{\text{particle}},95\%}=3t_{0}(V_{u}-\Delta V)+3t_{0}\Delta V(1-e^{-3})$

$x_{{\text{particle}},95\%}=3t_{0}(V_{u}-0.05\Delta V)$

Bu durum, parçacık hızının, şok dalgasından itibaren $x_{{\text{particle}},95\%}$ mesafede aşağı akış hızının $\%5$'ine yerleşeceği anlamına gelir. Pratikte bu, bir PIV sistemi için şok dalgasının yaklaşık olarak bu $x_{{\text{particle}},95\%}$ mesafesi kadar bulanık görüneceği anlamına gelir.

Örneğin, durgunluk sıcaklığı 298 K ve Mach sayısı $M=2$ olan normal bir şok dalgasını düşünelim. $d_{p}=1~\mu {\text{m}}$ çapındaki bir propilen glikol parçacığı, akışı $x_{{\text{particle}},95\%}=5{\text{ mm}}$ kadar bulanıklaştıracaktır; oysa $d_{p}=10~\mu {\text{m}}$ çapındaki bir parçacık, akışı $x_{{\text{particle}},95\%}=500{\text{ mm}}$ kadar bulanıklaştıracaktır (bu, çoğu durumda kabul edilemez PIV sonuçları verecektir).

Bir şok dalgası, akışın ani yavaşlamasının en kötü senaryosu olmasına rağmen, PIV'deki parçacık izleme hatasının etkisini ve bu hatanın hız alanlarının $x_{{\text{particle}},95\%}$ mertebesindeki uzunluk ölçeklerinde bulanıklaşmasına neden olduğunu gösterir.

Non-Stokesian sürükleme rejimi

Önceki analiz, ultra-Stokesian rejiminde doğru olmayacaktır, yani parçacık Reynolds sayısı birden çok daha büyük olduğunda geçerli değildir. Mach sayısının birlikten çok daha küçük olduğunu varsayarak, Israel ve Rosner tarafından genelleştirilmiş bir Stokes sayısı formu gösterilmiştir.

$${\text{Stk}}{\text{e}}={\text{Stk}}{\frac {24}{{\text{Re}}{o}}}\int _{0}^{{\text{Re}}_{o}}{\frac {d{\text{Re}}^{\prime }}{C_{D}({\text{Re}}^{\prime }){\text{Re}}^{\prime }}}$$

Burada ${\text{Re}}_{o}$, "parçacık serbest-akış Reynolds sayısı" olarak tanımlanır,

$${\text{Re}}_{o}={\frac {\rho _{g}|\mathbf {u} |d_{p}}{\mu _{g}}}$$

Ek olarak tanımlanan fonksiyon $\psi ({\text{Re}}_{o})$ ise; non-Stokesian sürükleme düzeltme faktörünü ifade eder,

$${\text{Stk}}{e}={\text{Stk}}\cdot \psi ({\text{Re}}{o})$$

Bu fonksiyon şu şekilde tanımlanır,

$\psi$, küresel bir parçacık için non-Stokesian sürükleme düzeltme faktörünü tanımlar

$$\psi ({\text{Re}}{o})={\frac {24}{{\text{Re}}{o}}}\int _{0}^{{\text{Re}}_{o}}{\frac {d{\text{Re}}^{\prime }}{C_{D}({\text{Re}}^{\prime }){\text{Re}}^{\prime }}}$$

Sınırlandırıcı parçacık serbest-akış Reynolds sayıları dikkate alındığında, ${\text{Re}}{o}\to 0$ olduğunda $C_{D}({\text{Re}}{o})\to 24/{\text{Re}}_{o}$ ve dolayısıyla $\psi \to 1$ olur. Bu nedenle, beklenildiği gibi Stokesian sürükleme rejiminde düzeltme faktörü birdir. Wessel & Righi $\psi$'yi Schiller & Naumann'ın bir küre üzerindeki sürükleme için ampirik korelasyonundan $C_{D}({\text{Re}})$ kullanarak değerlendirmiştir.

$$\psi ({\text{Re}}{o})={\frac {3({\sqrt {c}}{\text{Re}}{o}^{1/3}-\arctan({\sqrt {c}}{\text{Re}}{o}^{1/3}))}{c^{3/2}{\text{Re}}{o}}}$$

Burada sabit $c=0.158$ olarak alınmıştır. Geleneksel Stokes sayısı, büyük parçacık serbest-akış Reynolds sayıları için sürükleme kuvvetini önemli ölçüde küçümseyecektir. Bu da parçacıkların akış yönünden sapma eğilimini fazla tahmin edecektir. Bu durum, sonraki hesaplamalarda veya deneysel karşılaştırmalarda hatalara yol açacaktır.

Anizokinetik parçacık örneklemesinin uygulanması

Örneğin, Belyaev ve Levin tarafından tanımlanan hizalanmış, ince duvarlı dairesel bir nozul aracılığıyla parçacıkların seçici olarak yakalanması şu şekilde ifade edilmektedir:

$c/c_{0}=1+(u_{0}/u-1)\left(1-{\frac {1}{1+\mathrm {Stk} (2+0.617u/u_{0})}}\right)$

burada $c$ parçacık konsantrasyonu, $u$ hız ve alt simge 0, nozulun oldukça yukarısındaki koşulları belirtir. Karakteristik mesafe nozulun çapıdır. Bu durumda Stokes sayısı şu şekilde hesaplanır,

$\mathrm {Stk} ={\frac {u_{0}V_{s}}{dg}}$

burada $V_{s}$ parçacığın çökelme hızı, $d$ örnekleme tüpünün iç çapı ve $g$ yerçekimi ivmesidir.

Ayrıca bakınız

• Stokes yasası – Reynolds sayısı birden küçük olan parçacıklar üzerindeki akışkanlarda sürükleme kuvvetini ifade eder.

Diğer okumalar

• Fuchs, N. A. (1989). The mechanics of aerosols. New York: Dover Publications. ISBN 978-0-486-66055-4. 
• Hinds, William C. (1999). Aerosol technology: properties, behavior, and measurement of airborne particles. New York: Wiley. ISBN 978-0-471-19410-1. 
• Snyder, WH; Lumley, JL (1971). "Some Measurements of Particle Velocity Autocorrelation Functions in a Turbulent Flow". Journal of Fluid Mechanics. Cilt 48. ss. 41-71. Bibcode:1971JFM....48...41S. doi:10.1017/S0022112071001460. 
• Collins, LR; Keswani, A (2004). "Reynolds number scaling of particle clustering in turbulent aerosols". New Journal of Physics. 6 (119). s. 119. Bibcode:2004NJPh....6..119C. doi:10.1088/1367-2630/6/1/119 .