Orta Çağ İslam matematiği

Ebû Ca'fer Muhammed bin Mûsâ el-Hârizmî'nin *Cebir ve Denklem Hesabı Üzerine Özet Kitap (Arapça: El'Kitab'ül-Muhtasar fi Hısab'il Cebri ve'l-Mukabele, İngilizce: The Compendious Book on Calculation by Completion and Balancing)* adlı eserinden bir sayfa

İslam'ın Altın Çağı'nda matematik, özellikle 9. ve 10. yüzyıllarda, Yunan matematiği (Öklid, Arşimet, Apollonius) ve Hint matematiği (Aryabhata, Brahmagupta) üzerine inşa edilmiştir. Ondalık basamak-değer sisteminin ondalık kesirleri içerecek şekilde tam olarak geliştirilmesi, ilk sistematik cebir çalışması (Hârizmî tarafından yazılan Cebir ve Denklem Hesabı Üzerine Özet Kitap (Arapça: El'Kitab'ül-Muhtasar fi Hısab'il Cebri ve'l-Mukabele, İngilizce: The Compendious Book on Calculation by Completion and Balancing) adlı eser ve geometri ve trigonometride önemli ilerlemeler kaydedilmiştir.^[1]

Arap eserleri, aynı zamanda matematiğin 10. yüzyıldan 12. yüzyıla kadar Avrupa'ya aktarılmasında önemli bir rol oynadı.^[2]

İslam bilim tarihçisi Dr. Sally P. Ragep, matematik bilimleri ve felsefe alanındaki "on binlerce" Arapça el yazmasının hala okunmadığını, "bireysel önyargıları yansıtan ve nispeten az sayıda metin ve bilim adamı ile sınırlı bir odaklanma" olduğunu tahmin ediyor.^[3]

Kavramlar

Tahran Üniversitesi'nde bulunan Ömer Hayyam'ın *Konik kesitlerin kübik denklemleri ve kesişimleri (İngilizce: Cubic equations and intersections of conic sections)* adlı eserinin iki bölümlü el yazmasının ilk sayfası

Cebir

Adı tamamlama veya "kırık parçaların yeniden birleşmesi"^[4] anlamına gelen Arapça kelimeden türetilen cebir ile ilgili çalışmalar, İslam'ın Altın Çağı'nda parladı ve gelişti. Bağdat'taki Beyt'ül Hikmet (House of Wisdom)'de bir alim olan Hârizmî, Yunan matematikçi Diophantus ile birlikte cebirin babası olarak bilinir. Harizmi, Cebir ve Denklem Hesabı Üzerine Özet Kitap (Arapça: El'Kitab'ül-Muhtasar fi Hısab'il Cebri ve'l-Mukabele, İngilizce: The Compendious Book on Calculation by Completion and Balancing) adlı kitabında, birinci ve ikinci derece (doğrusal ve ikinci dereceden) polinom denklemlerinin pozitif köklerini çözmenin yollarını ele alır. Ayrıca indirgeme yöntemini tanıtır ve Diophantus'un aksine, ilgilendiği denklemlere genel çözümler sunar.^[5]^[6]^[7]

Harizmi'nin cebiri retorikti, yani denklemler tam cümlelerle yazılmıştı. Bu, Diophantus'un aksak ritimli cebirsel çalışmasından farklıydı, yani bazı semboller kullanıldı. Yalnızca sembollerin kullanıldığı sembolik cebire geçiş, İbnü’l-Bennâ el-Merrâküşî ve Ebu el-Hasan bin Ali el-Kalasadi'nın çalışmalarında görülebilir.^[7]^[8]

J. J. O'Connor ve Edmund F. Robertson el-Hârizmî'nin çalışmaları hakkında:^[9]

“	"Arap matematiğinin belki de en önemli gelişmelerinden biri bu dönemde Harizmi'nin çalışmasıyla, yani cebirin başlangıcıyla başladı. Bu yeni fikrin ne kadar önemli olduğunu anlamak önemlidir. Bu, esasen geometri olan Yunan matematik kavramından uzaklaşmak için devrim niteliğinde bir hareketti. Cebir, rasyonel sayılar, irrasyonel sayıların, geometrik büyüklüklerin vb. Hepsinin "cebirsel nesneler" olarak değerlendirilmesine izin veren birleştirici bir teoriydi. Matematiğe, kavram olarak daha önce var olandan çok daha geniş yepyeni bir gelişim yolu verdi ve konunun gelecekteki gelişimi için bir araç sağladı. Cebirsel fikirlerin tanıtılmasının bir diğer önemli yönü, matematiğin daha önce olmadığı bir şekilde kendisine uygulanmasına izin vermesiydi."	„
— MacTutor History of Mathematics archive

şeklinde konuşmuşlardır.

Bu dönemde diğer birkaç matematikçi Harizmi'nin cebirini genişletti. Ebu Kamil Şüca bin Aslam, geometrik çizimler ve ispatlar eşliğinde bir cebir kitabı yazdı. Ayrıca bazı sorunlarının olası tüm çözümlerini de sıraladı. Muhammed bin Ahmed bin el-Layth, Ömer Hayyam, Şerafeddin el-Tusî ile birlikte kübik denklemin birkaç çözümünü buldu. Ömer Hayyam, kübik bir denklemin genel geometrik çözümünü buldu.

Kübik denklemler

Ömer Hayyam (yaklaşık 1038/48, İran - 1123/24)^[10] Hârizmî'nin cebirinin ötesine geçen kübik veya üçüncü mertebeden denklemlerin sistematik çözümünü içeren Cebir Problemlerinin Gösterilmesi Üzerine İnceleme (İngilizce: Treatise on Demonstration of Problems of Algebra) 'yi yazdı.^[11] Hayyam, iki konik kesitin kesişme noktalarını bularak bu denklemlerin çözümlerini elde etti. Bu yöntem Yunanlar tarafından kullanılmıştı^[12] ancak tüm denklemleri pozitif köklerle kapsayacak şekilde genelleştirmediler.^[11]

Hayyam, "geometrik" ve "aritmetik" çözümleri birbirinden ayırdı.^[12] Hayyam, hatalı olarak^[11] aritmetik çözümlerin yalnızca denklem kökleri pozitif ve rasyonel sayı olması durumunda var olduğuna inanıyordu.^[12] Hayyam, çözümlerin sayısal hesaplamalarıyla ilgilenmedi.^[12] ^{[not 1]}

Şerafeddin el-Tusî (? Tus, İran - 1213/4) kübik denklemlerin incelenmesine, kübik bir polinomun maksimum değerini elde ettiği noktayı bulmayı gerektiren yeni bir yaklaşım geliştirdi. Örneğin, a ve b pozitif olan $\ x^{3}+a=bx$ denklemini çözmek için, $\ y=bx-x^{3}$ eğrisinin maksimum noktasını $x=\textstyle {\sqrt {\frac {b}{3}}}$ konumunda bulunur ve o noktadaki eğrinin yüksekliğinin a'dan küçük, eşit veya daha büyük olmasına bağlı olarak denklemin hiçbir çözümü olmayacağını, bir çözümü veya iki çözümü olacağını söylemek mümkündür. Günümüze ulaşan çalışmaları, bu eğrilerin maksimumları için formüllerini nasıl keşfettiğine dair hiçbir ipucu vermemektedir. Bunları keşfetmesine dair açıklama getirmek için çeşitli varsayımlar öne sürülmüştür.^[13]

Tümevarım

Matematiksel tümevarımın en eski örtük izleri Öklid'in asal sayıların sonsuz olduğunun kanıtı olarak geliştirdiği Öklid teoremi'nde bulunabilir (yaklaşık MÖ 300). Tümevarım ilkesinin ilk açık formülasyonu, Blaise Pascal tarafından 1665 yılında Aritmetik Üçgen üzerine inceleme (Fransızca: Traité du triangle arithmétique) adlı eserinde vermiştir.

Aritmetik diziler için tümevarım yoluyla örtük ispat ise Kerecî tarafından tanıtıldı (yaklaşık 1000) ve bunu binom teoreminin özel durumları ve Pascal üçgeninin özellikleri için kullanan Semev’el el-Mağribî tarafından devam ettirildi.

İrrasyonel sayılar

Yunanlar irrasyonel sayıları keşfetmişlerdi, ancak onlardan memnun değillerdi ve yalnızca "büyüklük" ve "sayı" arasında bir ayrım yaparak irrasyonel sayılarla başa çıkabildiler. Yunan görüşünde, "büyüklükler" sürekli olarak değişiyordu ve çizgi parçaları gibi varlıklar için kullanılabilirken, "sayılar" ayrık idi. Dolayısıyla irrasyoneller yalnızca geometrik olarak ele alınabilirdi ve gerçekten de Yunan matematiği esas olarak geometrikti. Ebu Kamil Şüca bin Aslam ve Abdülkāhir el-Bağdâdî gibi İslami matematikçiler, büyüklük ve sayı arasındaki ayrımı yavaşça ortadan kaldırarak irrasyonel büyüklüklerin denklemlerde katsayılar olarak görünmesine ve cebirsel denklemlerin çözümleri olmasına izin verdi.^[14]^[15] Matematiksel nesneler olarak irrasyonellerle özgürce çalıştılar, ancak doğalarını yakından incelemediler.^[16]

12. yüzyılda, Harizmi'nin Hint rakamları üzerindeki Aritmetiğinin (Arapça: Kitab fi usul hisab al-hind, Hindu Hesaplamalarının İlkeleri adlı eseri) Latince tercümeleri, ondalık konumsal sayı sistemini Batı dünyasına tanıttı.^[17] Cebir ve Denklem Hesabı Üzerine Özet Kitap (Arapça: El'Kitab'ül-Muhtasar fi Hısab'il Cebri ve'l-Mukabele, İngilizce: The Compendious Book on Calculation by Completion and Balancing) adlı eseri, doğrusal ve ikinci dereceden denklemlerin ilk sistematik çözümlerini sundu. Rönesans Avrupa'sında, çalışmalarının eski Hint veya Yunan kaynaklarına dayandığı artık bilinmesine rağmen, cebrin orijinal mucidi olarak kabul edildi.^[18] Batlamyus'un Coğrafya (İngilizce: Geography) 'sını gözden geçirdi ve astronomi ile astroloji üzerine yazdı. Ancak, C.A. Nallino, Hârizmi'nin orijinal çalışmasının Batlamyus'a değil, muhtemelen Süryanice veya Arapça bir kaynaktan türetilmiş bir dünya haritasına^[19] dayandığını öne sürer.

Küresel trigonometri

Küresel sinüs yasası, 10. yüzyılda keşfedildi: çeşitli şekillerde Hucendî, Nasîrüddin Tûsî ve Ebu Nasr Mansur'a, katkıda bulunan kişi olarak Ebu'l-Vefâ el-Bûzcânî'ye atfedildi.^[14] İbn Mu'az el-Ceyyani'nin 11. yüzyılda bir kürenin bilinmeyen yayları kitabında genel sinüs yasasını tanıttı.^[20] Sinüslerin düzlem yasası 13. yüzyılda Nasîrüddin Tûsî tarafından tanımlanmıştır. On the Sector Figure adlı eserinde düzlem ve küresel üçgenler için sinüs yasasını belirtmiş ve bu yasaya kanıtlar sağlamıştır.^[21]

Negatif sayılar

9. yüzyılda İslami matematikçiler Hint matematikçilerin çalışmalarındaki negatif sayılara aşinaydı, ancak bu dönemde negatif sayıların tanınması ve kullanılması konusunda çekingen kalındı.^[22] Hârizmi, negatif sayılar veya negatif katsayılar kullanmadı.^[22] Ancak elli yıl içinde Ebu Kamil Şuca, $(a\pm b)(c\pm d)$ çarpımını genişletmek için işaretlerin kurallarını açıkladı.^[23] El-Kerecî, al-Fakhrī adlı kitabında "negatif miktarların terim olarak sayılması gerektiğini" yazdı.^[22] 10. yüzyılda Ebu'l-Vefâ el-Bûzcânî, Aritmetik Biliminden Yazanlar ve İşadamları İçin Gerekli Olanlar Üzerine Bir Kitap (İngilizce: A Book on What Is Necessary from the Science of Arithmetic for Scribes and Businessmen) 'ta borçları negatif sayılar olarak kabul etti.^[23]

12. yüzyılda, El-Kerecî'nin halefleri işaretlerin genel kurallarını belirtecek ve bunları, polinom bölünmelerini çözmek için kullanacaklardı.^[22] Semev'el el-Mağribî'nin yazdığı gibi:

“	negatif bir sayının - al-nāqiṣ - pozitif bir sayı ile - al-zāʾid - çarpımı negatiftir ve negatif bir sayı ile çarpımı pozitiftir. Negatif bir sayıyı daha yüksek bir negatif sayıdan çıkarırsak, geri kalan onların negatif farkıdır. Negatif bir sayıyı daha düşük bir negatif sayıdan çıkarırsak, fark pozitif kalır. Pozitif bir sayıdan negatif bir sayıyı çıkarırsak, geri kalan onların pozitif toplamıdır. Boş bir kuvvetten (martaba khāliyya) pozitif bir sayı çıkarırsak, geri kalan aynı negatiftir ve boş bir kuvvetten negatif bir sayı çıkarırsak, geri kalan aynı pozitif sayıdır.^[22]	„

Çift yanlış yöntemi

9. ve 10. yüzyıllar arasında Mısırlı matematikçi Ebu Kamil Şuca, İki Hatanın Kitabı (Arapça: Kitâbü’l-Ḫaṭaʾeyn) olarak bilinen çift yanlış yönteminin kullanımı üzerine şimdi kaybolmuş olan bir inceleme yazdı. Orta Doğu'dan çift yanlış yöntemi üzerine günümüze ulaşan en eski yazı, Lübnan'ın Baalbek şehrinden bir Arap matematikçi olan Kusta bin Luka'ya (10. yüzyıl) aittir. Tekniği, Öklidci tarzda muntazam bir geometrik ispat yöntemiyle doğruladı. Orta Çağ Müslüman matematiği geleneğinde, çift yanlış yöntemi, hesab'ül haṭaʾeyn ("iki hatayla hesaplaşma", "reckoning by two errors") olarak biliniyordu. Yüzyıllar boyunca ticari ve hukuki sorunlar (Kuran'daki miras kurallarına göre mülk paylaşımı) ve tamamen eğlence problemleri gibi pratik problemleri çözmek için kullanıldı. Algoritma genellikle, Fas kökenli matematikçiler olan İbn Haccâc el-İşbîlî'ye atfedilen bir dize ve Ebû Bekir bin Ayyâş ile İbnü’l-Bennâ el-Merrâküşî tarafından açıklanan denge-ölçekli diyagramlar gibi anımsatıcılar yardımıyla ezberlendi.^[24]

Diğer önemli şahıslar

Abdülhamîd bin Vâsi bin Türk (830 dolayları) (kuadratikler)
Sabit bin Kurra (826–901)
Sind ibn Ali (ö. 864 sonrası)
Cezeri (1136–1206)
Kuhi (yaklaşık 940–1000) (ağırlık merkezleri)
Ebu'l-Hasan el-Uklidisi (952–953) (aritmetik)
El-Kabîsî (ö. 967)
İbn-i Heysem (yaklaşık 965–1040)
Birûni (973–1048) (trigonometri)
İbn Madâ (yaklaşık 1116–1196)
Gıyaseddin Cemşid (yaklaşık 1380–1429) (ondalık sayılar ve daire sabitinin tahmini)

Galeri

İslam'ın Altın Çağında Matematik

Konik kesitler çizmek için Kuhi'nin mükemmel pergelinin gravürü.
İbnü'l-Heysem (Alhazen) Problemi.
Tûsî çifti (Vatikan Kütüphanesi, Vatikan Arşivi, Arabic ms 319)
Tûsî çiftinin animasyon modeli.
Sabit bin Kurra'nın Apollonius'un Konikler adlı eserinin Arapça çevirisinden sayfalar
Siczi'nin geometrik incelemesinden bir sayfa.
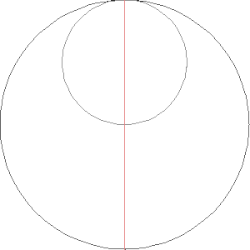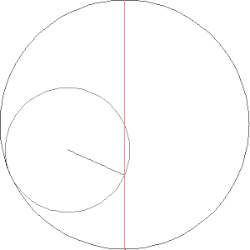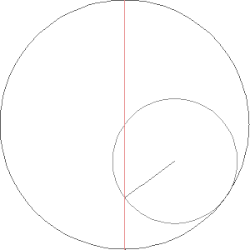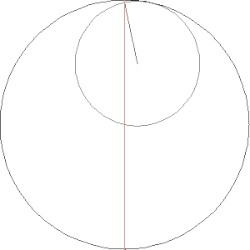
Ömer Hayyam'ın $x^{3}+2x=2x^{2}+2$ Kübik denklem için bir çözüm oluşturması. Daire ve hiperbol tarafından üretilen kesişme noktası istenen parçayı belirler.

Notlar

^ Katz (1993): "Orta Çağ İslamının tam bir matematik tarihi henüz yazılamaz, çünkü bu Arapça el yazmalarının pek çoğu incelenmemiş durumda ... Yine de, genel taslak ... biliniyor. Özellikle, İslami matematikçiler, ondalık kesirleri içerecek şekilde ondalık basamak-değer sayı sistemini tamamen geliştirdiler, cebir çalışmalarını sistematik hale getirdiler ve cebir ve geometri arasındaki ilişkiyi düşünmeye başladılar, Öklid, Arşimet ve Apollonius'un başlıca Yunan geometrik incelemeleri üzerinde çalıştılar, ilerlemeler kaydettiler ve düzlem ve küresel geometride önemli gelişmeler sağladılar." Smith (1958) Cilt. 1, Bölüm VII.4: "Genel olarak Arap matematiğinin Altın Çağı'nın büyük ölçüde 9. ve 10. yüzyıllarla sınırlı olduğu söylenebilir; Yunan matematiğinin klasiklerini korumak ve gelecek nesillere aktarmak için dünyanın Arap bilim adamlarına büyük bir borcu olduğunu ve cebirde hatırı sayılır bir özgünlük geliştirmelerine ve trigonometri çalışmalarında biraz deha göstermelerine rağmen, çalışmalarının esas olarak aktarım işi olduğunu söylemek mümkündür."
^ Adolph P. Yushkevich Sertima, Ivan Van (1992), Golden age of the Moor, Volume 11, Transaction Publishers, s. 394, ISBN 1-56000-581-5 "İslâm matematikçileri, Avrupa'da bilimin gelişmesi üzerinde, Yunanlar, Hintler, Suriyeliler, Babilliler vb. tarafından miras aldıkları kadar, kendi keşifleriyle de zenginleştirerek verimli bir etki yaptılar."
^ "Science Teaching in Pre-Modern Societies". McGill University. 11 Mayıs 2018 tarihinde kaynağından arşivlendi.
^ "algebra". Online Etymology Dictionary. 14 Mayıs 2005 tarihinde kaynağından arşivlendi. Erişim tarihi: 28 Ağustos 2020.
^ Boyer, Carl B. (1991). "The Arabic Hegemony". A History of Mathematics (2. bas.). John Wiley & Sons. s. 228. ISBN 0-471-54397-7.
^ Swetz, Frank J. (1993). Learning Activities from the History of Mathematics. Walch Publishing. s. 26. ISBN 978-0-8251-2264-4. 24 Aralık 2018 tarihinde kaynağından arşivlendi. Erişim tarihi: 28 Ağustos 2020.
^ ^a ^b Gullberg, Jan (1997). Mathematics: From the Birth of Numbers. W. W. Norton. s. 298. ISBN 0-393-04002-X.
^ O'Connor, John J.; Robertson, Edmund F., "al-Marrakushi ibn Al-Banna", MacTutor Matematik Tarihi arşivi
^ O'Connor, John J.; Robertson, Edmund F., "Arabic mathematics: forgotten brilliance?", MacTutor Matematik Tarihi arşivi
^ Struik 1987, s. 96.
^ ^a ^b ^c ^d Boyer 1991, ss. 241–242.
^ ^a ^b ^c ^d Struik 1987, s. 97.
^ Berggren, J. Lennart; Al-Tūsī, Sharaf Al-Dīn; Rashed, Roshdi (1990). "Innovation and Tradition in Sharaf al-Dīn al-Ṭūsī's al-Muʿādalāt". Journal of the American Oriental Society. 110 (2): 304–309. doi:10.2307/604533. JSTOR 604533.
^ ^a ^b Sesiano, Jacques (2000). Helaine, Selin; Ubiratan, D'Ambrosio (Ed.). Islamic mathematics. Mathematics Across Cultures: The History of Non-western Mathematics. Springer. ss. 137-157. ISBN 1-4020-0260-2.
^ O'Connor, John J.; Robertson, Edmund F., "Abu Mansur ibn Tahir Al-Baghdadi", MacTutor Matematik Tarihi arşivi
^ Allen, G. Donald (n.d.). "The History of Infinity" (PDF). Texas A&M University. 30 Ağustos 2000 tarihinde kaynağından (PDF) arşivlendi. Erişim tarihi: 7 Eylül 2016.
^ Struik 1987, s. 93
^ Rosen 1831, s. v–vi; Toomer 1990
^ Nallino (1939).
^ O'Connor, John J.; Robertson, Edmund F., "Abu Abd Allah Muhammad ibn Muadh Al-Jayyani", MacTutor Matematik Tarihi arşivi
^ Berggren, J. Lennart (2007). "Mathematics in Medieval Islam". The Mathematics of Egypt, Mesopotamia, China, India, and Islam: A Sourcebook. Princeton University Press. s. 518. ISBN 978-0-691-11485-9.
^ ^a ^b ^c ^d ^e Rashed, R. (30 Haziran 1994). The Development of Arabic Mathematics: Between Arithmetic and Algebra. Springer. ss. 36-37. ISBN 9780792325659.
^ ^a ^b Mat Rofa Bin Ismail (2008), Helaine Selin (Ed.), "Algebra in Islamic Mathematics", Encyclopaedia of the History of Science, Technology, and Medicine in Non-Western Cultures, 2., Springer, 1, s. 115, ISBN 9781402045592
^ Schwartz, R. K. (2004). Issues in the Origin and Development of Hisab al-Khata’ayn (Calculation by Double False Position). Eighth North African Meeting on the History of Arab Mathematics. Radès, Tunisia. Available online at: "Issues in the Origin and Development of Hisab al-Khata'ayn (Calculation by Double False Position)". 15 Eylül 2011 tarihinde kaynağından arşivlendi. and "Archived copy" (PDF). 16 Mayıs 2014 tarihinde kaynağından (PDF) arşivlendi. Erişim tarihi: 8 Haziran 2012.

Dipnotlar

^ "Ömer Hayyam, 'Çadırcı' (yaklaşık 1050–1123), üçüncü dereceden denklemleri içerecek şekilde Harizmi'nin ötesine geçen bir "Cebir" yazdı. Selefleri gibi Ömer Hayyam, ikinci dereceden denklemler için hem aritmetik hem de geometrik çözümler sağladı; genel kübik denklemler için (yanlışlıkla, on altıncı yüzyılın daha sonra gösterdiği gibi) aritmetik çözümlerin imkansız olduğuna inandı; bu nedenle yalnızca geometrik çözümler verdi. Kübikleri çözmek için kesişen koniklerin kullanılması yöntemi, daha önce Menaechmus, Arşimet ve İbn-i Heysem tarafından kullanılmıştı, ancak Ömer Hayyam, (pozitif kökleri olan) üçüncü derece denklemleri kapsayacak şekilde genelleştirme yönteminde övgüye değer bir adım attı. [...] Üçten daha yüksek dereceli denklemler için, Ömer Hayyam görünüşe göre benzer geometrik yöntemler öngörmedi, çünkü uzay üç boyuttan fazlasını içermiyordu, [...]"^[11]

Kaynakça

Boyer, Carl B. (1991), "Greek Trigonometry and Mensuration, and The Arabic Hegemony", A History of Mathematics, 2., New York City: John Wiley & Sons, ISBN 0-471-54397-7
Nallino, C.A. (1939), "Al-Ḥuwārismī e il suo rifacimento della Geografia di Tolomeo", Raccolta di scritti editi e inediti, V, Rome: Istituto per l'Oriente, ss. 458-532 . (İtalyanca)
Struik, Dirk J. (1987), A Concise History of Mathematics, 4., Dover Publications, ISBN 0-486-60255-9

Konuyla ilgili yayınlar

İslam matematiği üzerine kitaplar

Berggren, J. Lennart (1986). Episodes in the Mathematics of Medieval Islam. New York: Springer-Verlag. ISBN 0-387-96318-9.
- Review: Toomer, Gerald J.; Berggren, J. L. (1988). "Episodes in the Mathematics of Medieval Islam". American Mathematical Monthly. Mathematical Association of America. 95 (6): 567. doi:10.2307/2322777. JSTOR 2322777.
- Review: Hogendijk, Jan P.; Berggren, J. L. (1989). "Episodes in the Mathematics of Medieval Islam by J. Lennart Berggren". Journal of the American Oriental Society. American Oriental Society. 109 (4): 697-698. doi:10.2307/604119. JSTOR 604119.
Daffa', Ali Abdullah al- (1977). The Muslim contribution to mathematics. Londra: Croom Helm. ISBN 0-85664-464-1.
Katz, Victor J. (1993). A History of Mathematics: An Introduction. HarperCollins college publishers. ISBN 0-673-38039-4.
Ronan, Colin A. (1983). The Cambridge Illustrated History of the World's Science. Cambridge University Press. ISBN 0-521-25844-8.
Smith, David E. (1958). History of Mathematics. Dover Publications. ISBN 0-486-20429-4.
Rashed, Roshdi (2001). The Development of Arabic Mathematics: Between Arithmetic and Algebra. Translated by A. F. W. Armstrong. Springer. ISBN 0-7923-2565-6.
Rosen, Fredrick (1831). The Algebra of Mohammed Ben Musa. Kessinger Publishing. ISBN 1-4179-4914-7.
Toomer, Gerald (1990). "Al-Khwārizmī, Abu Ja'far Muḥammad ibn Mūsā". Gillispie, Charles Coulston (Ed.). Dictionary of Scientific Biography. 7. New York: Charles Scribner's Sons. ISBN 0-684-16962-2. 2 Temmuz 2016 tarihinde kaynağından arşivlendi. Erişim tarihi: 28 Ağustos 2020.
Youschkevitch, Adolf P.; Rozenfeld, Boris A. (1960). Die Mathematik der Länder des Ostens im Mittelalter. Berlin. Sowjetische Beiträge zur Geschichte der Naturwissenschaft pp. 62–160.
Youschkevitch, Adolf P. (1976). Les mathématiques arabes: VIII^e–XV^e siècles. translated by M. Cazenave and K. Jaouiche. Paris: Vrin. ISBN 978-2-7116-0734-1.

İslam matematiği üzerine kitap bölümleri

Berggren, J. Lennart (2007). "Mathematics in Medieval Islam". Victor J. Katz (Ed.). The Mathematics of Egypt, Mesopotamia, China, India, and Islam: A Sourcebook (Second bas.). Princeton, New Jersey: Princeton University. ISBN 978-0-691-11485-9.
Cooke, Roger (1997). "Islamic Mathematics". The History of Mathematics: A Brief Course. Wiley-Interscience. ISBN 0-471-18082-3.

İslam bilimi üzerine kitaplar

Daffa, Ali Abdullah al-; Stroyls, J.J. (1984). Studies in the exact sciences in medieval Islam. New York: Wiley. ISBN 0-471-90320-5.
Kennedy, E. S. (1984). Studies in the Islamic Exact Sciences. Syracuse Univ Press. ISBN 0-8156-6067-7.

Matematik tarihi üzerine kitaplar

Joseph, George Gheverghese (2000). The Crest of the Peacock: Non-European Roots of Mathematics (2. bas.). Princeton University Press. ISBN 0-691-00659-8. (Reviewed: Katz, Victor J.; Joseph, George Gheverghese (1992). "The Crest of the Peacock: Non-European Roots of Mathematics by George Gheverghese Joseph". The College Mathematics Journal. Mathematical Association of America. 23 (1): 82-84. doi:10.2307/2686206. JSTOR 2686206. )
Youschkevitch, Adolf P. (1964). Gesichte der Mathematik im Mittelalter. Leipzig: BG Teubner Verlagsgesellschaft.

İslam matematiği üzerine dergi makaleleri

Høyrup, Jens. “The Formation of «Islamic Mathematics»: Sources and Conditions” 19 Temmuz 2011 tarihinde Wayback Machine sitesinde arşivlendi.. Filosofi og Videnskabsteori på Roskilde Universitetscenter. 3. Række: Preprints og Reprints 1987 Nr. 1.

Bibliyografyalar ve biyografiler

Brockelmann, Carl. Geschichte der Arabischen Litteratur. 1.–2. Band, 1.–3. Supplementband. Berlin: Emil Fischer, 1898, 1902; Leiden: Brill, 1937, 1938, 1942.
Sánchez Pérez, José A. (1921). Biografías de Matemáticos Árabes que florecieron en España. Madrid: Estanislao Maestre.
Sezgin, Fuat (1997). Geschichte Des Arabischen Schrifttums (Almanca). Brill Academic Publishers. ISBN 90-04-02007-1.
Suter, Heinrich (1900). Die Mathematiker und Astronomen der Araber und ihre Werke. Abhandlungen zur Geschichte der Mathematischen Wissenschaften Mit Einschluss Ihrer Anwendungen, X Heft. Leipzig.

Televizyon belgeselleri

Marcus du Sautoy (presenter) (2008). "The Genius of the East". The Story of Maths. BBC.
Jim Al-Khalili (presenter) (2010). Science and Islam. BBC.

Dış bağlantılar

Hogendijk, Jan P. (Ocak 1999). "Bibliography of Mathematics in Medieval Islamic Civilization". 31 Ocak 2011 tarihinde kaynağından arşivlendi. Erişim tarihi: 28 Ağustos 2020.
O'Connor, John J.; Robertson, Edmund F., "Arabic mathematics: forgotten brilliance?", MacTutor Matematik Tarihi arşivi
Richard Covington (2007). "Rediscovering Arabic Science". Saudi Aramco World. 30 Ekim 2014 tarihinde kaynağından arşivlendi.
"İslam'ın Altın Çağında Matematikteki Buluş ve Keşiflerin Listesi". 14 Şubat 2020 tarihinde kaynağından arşivlendi.

[1] Katz (1993): "Orta Çağ İslamının tam bir matematik tarihi henüz yazılamaz, çünkü bu Arapça el yazmalarının pek çoğu incelenmemiş durumda ... Yine de, genel taslak ... biliniyor. Özellikle, İslami matematikçiler, ondalık kesirleri içerecek şekilde ondalık basamak-değer sayı sistemini tamamen geliştirdiler, cebir çalışmalarını sistematik hale getirdiler ve cebir ve geometri arasındaki ilişkiyi düşünmeye başladılar, Öklid, Arşimet ve Apollonius'un başlıca Yunan geometrik incelemeleri üzerinde çalıştılar, ilerlemeler kaydettiler ve düzlem ve küresel geometride önemli gelişmeler sağladılar." Smith (1958) Cilt. 1, Bölüm VII.4: "Genel olarak Arap matematiğinin Altın Çağı'nın büyük ölçüde 9. ve 10. yüzyıllarla sınırlı olduğu söylenebilir; Yunan matematiğinin klasiklerini korumak ve gelecek nesillere aktarmak için dünyanın Arap bilim adamlarına büyük bir borcu olduğunu ve cebirde hatırı sayılır bir özgünlük geliştirmelerine ve trigonometri çalışmalarında biraz deha göstermelerine rağmen, çalışmalarının esas olarak aktarım işi olduğunu söylemek mümkündür."

[2] Adolph P. Yushkevich Sertima, Ivan Van (1992), Golden age of the Moor, Volume 11, Transaction Publishers, s. 394, ISBN 1-56000-581-5 "İslâm matematikçileri, Avrupa'da bilimin gelişmesi üzerinde, Yunanlar, Hintler, Suriyeliler, Babilliler vb. tarafından miras aldıkları kadar, kendi keşifleriyle de zenginleştirerek verimli bir etki yaptılar."

[3] "Science Teaching in Pre-Modern Societies". McGill University. 11 Mayıs 2018 tarihinde kaynağından arşivlendi.

[4] "algebra". Online Etymology Dictionary. 14 Mayıs 2005 tarihinde kaynağından arşivlendi. Erişim tarihi: 28 Ağustos 2020.

[5] Boyer, Carl B. (1991). "The Arabic Hegemony". A History of Mathematics (2. bas.). John Wiley & Sons. s. 228. ISBN 0-471-54397-7.

[6] Swetz, Frank J. (1993). Learning Activities from the History of Mathematics. Walch Publishing. s. 26. ISBN 978-0-8251-2264-4. 24 Aralık 2018 tarihinde kaynağından arşivlendi. Erişim tarihi: 28 Ağustos 2020.

[Gullberg-7] Gullberg, Jan (1997). Mathematics: From the Birth of Numbers. W. W. Norton. s. 298. ISBN 0-393-04002-X.

[8] O'Connor, John J.; Robertson, Edmund F., "al-Marrakushi ibn Al-Banna", MacTutor Matematik Tarihi arşivi

[9] O'Connor, John J.; Robertson, Edmund F., "Arabic mathematics: forgotten brilliance?", MacTutor Matematik Tarihi arşivi

[FOOTNOTEStruik198796-10] Struik 1987, s. 96.

[FOOTNOTEBoyer1991241–242-11] Boyer 1991, ss. 241–242.

[FOOTNOTEStruik198797-12] Struik 1987, s. 97.

[14] Berggren, J. Lennart; Al-Tūsī, Sharaf Al-Dīn; Rashed, Roshdi (1990). "Innovation and Tradition in Sharaf al-Dīn al-Ṭūsī's al-Muʿādalāt". Journal of the American Oriental Society. 110 (2): 304–309. doi:10.2307/604533. JSTOR 604533.

[Sesiano-15] Sesiano, Jacques (2000). Helaine, Selin; Ubiratan, D'Ambrosio (Ed.). Islamic mathematics. Mathematics Across Cultures: The History of Non-western Mathematics. Springer. ss. 137-157. ISBN 1-4020-0260-2.

[16] O'Connor, John J.; Robertson, Edmund F., "Abu Mansur ibn Tahir Al-Baghdadi", MacTutor Matematik Tarihi arşivi

[17] Allen, G. Donald (n.d.). "The History of Infinity" (PDF). Texas A&M University. 30 Ağustos 2000 tarihinde kaynağından (PDF) arşivlendi. Erişim tarihi: 7 Eylül 2016.

[Struik_93-18] Struik 1987, s. 93

[19] Rosen 1831, s. v–vi; Toomer 1990

[FOOTNOTENallino1939-20] Nallino (1939).

[MacTutor_Al-Jayyani-21] O'Connor, John J.; Robertson, Edmund F., "Abu Abd Allah Muhammad ibn Muadh Al-Jayyani", MacTutor Matematik Tarihi arşivi

[22] Berggren, J. Lennart (2007). "Mathematics in Medieval Islam". The Mathematics of Egypt, Mesopotamia, China, India, and Islam: A Sourcebook. Princeton University Press. s. 518. ISBN 978-0-691-11485-9.

[Rashed-23] Rashed, R. (30 Haziran 1994). The Development of Arabic Mathematics: Between Arithmetic and Algebra. Springer. ss. 36-37. ISBN 9780792325659.

[Ismail-24] Mat Rofa Bin Ismail (2008), Helaine Selin (Ed.), "Algebra in Islamic Mathematics", Encyclopaedia of the History of Science, Technology, and Medicine in Non-Western Cultures, 2., Springer, 1, s. 115, ISBN 9781402045592

[Schwartz-25] Schwartz, R. K. (2004). Issues in the Origin and Development of Hisab al-Khata’ayn (Calculation by Double False Position). Eighth North African Meeting on the History of Arab Mathematics. Radès, Tunisia. Available online at: "Issues in the Origin and Development of Hisab al-Khata'ayn (Calculation by Double False Position)". 15 Eylül 2011 tarihinde kaynağından arşivlendi. and "Archived copy" (PDF). 16 Mayıs 2014 tarihinde kaynağından (PDF) arşivlendi. Erişim tarihi: 8 Haziran 2012.

[13] "Ömer Hayyam, 'Çadırcı' (yaklaşık 1050–1123), üçüncü dereceden denklemleri içerecek şekilde Harizmi'nin ötesine geçen bir "Cebir" yazdı. Selefleri gibi Ömer Hayyam, ikinci dereceden denklemler için hem aritmetik hem de geometrik çözümler sağladı; genel kübik denklemler için (yanlışlıkla, on altıncı yüzyılın daha sonra gösterdiği gibi) aritmetik çözümlerin imkansız olduğuna inandı; bu nedenle yalnızca geometrik çözümler verdi. Kübikleri çözmek için kesişen koniklerin kullanılması yöntemi, daha önce Menaechmus, Arşimet ve İbn-i Heysem tarafından kullanılmıştı, ancak Ömer Hayyam, (pozitif kökleri olan) üçüncü derece denklemleri kapsayacak şekilde genelleştirme yönteminde övgüye değer bir adım attı. [...] Üçten daha yüksek dereceli denklemler için, Ömer Hayyam görünüşe göre benzer geometrik yöntemler öngörmedi, çünkü uzay üç boyuttan fazlasını içermiyordu, [...]"^[11]

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[not 1]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]

[24]

g t d Matematik tarihi
Konuya göre	Cebir zaman çizelgesi Algoritmalar zaman çizelgesi Aritmetik zaman çizelgesi Kalkülüs zaman çizelgesi Grandi serileri Kategori teorisi zaman çizelgesi Topos teorisi Kombinatorik Fonksiyonlar Logaritma Geometri Trigonometri zaman çizelgesi Grup teorisi Bilgi teorisi zaman çizelgesi Mantık zaman çizelgesi Matematik notasyonu Sayı teorisi zaman çizelgesi İstatistik zaman çizelgesi Olasılık Topoloji Manifoldlar zaman çizelgesi Ayırma aksiyomları
Sayısal sistemler	Tarih öncesi Antik Hint-Arap
Ülkelere ve kültürlere göre	Antik Mısır Babil Çin Antik Yunan Hint Ermenistan İnkalar İslam Rusya Afrika
Tartışmalar	Brouwer-Hilbert Cantor teorisi üzerine Leibniz-Newton Hobbes-Wallis
Diğer	Matematikte kadınlar zaman çizelgesi π yaklaşımları zaman çizelgesi Matematiğin geleceği
Ayrıca bakınız	Analitik geometri Diferansiyel geometri Fonksiyonel Analiz Fonksiyonlar İrrasyonel sayılar Karmaşık sayılar Kriptografi Küme teorisi Lineer cebir Matematik eğitimi Matematiksel analiz Matematiksel ispat Matematiksel mantık Negatif sayılar Matematiksel optimizasyon Öklid-dışı geometriler Reel sayılar Sonsuz küçük Sonsuz Sürekli kesirler Varyasyonlar hesabı
Matematiğin zaman çizelgesi

g t d Antik Yunan matematiği
Matematikçiler (Zaman Çizelgesi)	Anaksagoras Antemios Apollonios Arkhytas Aristaios Aristarkos Arşimet Autolykos Bion Boethius Brison Kallippos Karpos Kleomedes Konon Ktesibios Demokritos Dikaiarkhos Diokles Diophantos Dinostratus Dionisodoros Domninus Elealı Zenon Eratosthenes Eudemos Eudoksos Eutokios Geminus Heliodoros İskenderiyeli Heron Khrysippos Hipparkhos Hippasos Hippias Hipokrat Hipatia Hipsikles İsidoros Matematikçi Leo Leon Marinos Melissa Menaikhmos Menelaos Metrodoros Nikomakhos Nikomedes Nikoteles Oenopides Euklides Pappos Perseus Philolaos Philon Laodikyalı Philonides Porphyrios Poseidonios Proklos Batlamyus Pisagor Serenus Simplikios Sosigenes Sporus Thales Theaitetos Theano Teodoros Theodosios İskenderiyeli Theon Smirnalı Theon Timaridas Ksenokrates Sidonlu Zenon Zenodoros
Yapıtlar	Almagest Arşimet Parşömeni Arithmetika Konikler (Apollonius) Katoptrik (Yansımalar) Data (Öklid) Elemanlar (Öklid) Bir Çemberin Ölçümü Konikler ve Sferoidler Üzerine Büyüklükler ve Uzaklıklar Üzerine (Aristarkhos) Büyüklükler ve Uzaklıklar Üzerine (Hipparkhos) Hareketli Küre Üzerine (Autolykos) Öklid'in Optiği Sarmallar Üzerine Küre ve Silindir Üzerine Ostomachion (Syntomachion) Planisphaerium Sphaerics Parabolün Dörtgenleştirilmesi Kum Sayacı Sonsuz Küçükler Hesabı
Merkezler	Platon Akademisi · Kirene · İskenderiye Kütüphanesi
Etkilendikleri	Babil matematiği · Eski Mısır matematiği
Etkiledikleri	Avrupa matematiği · Hint matematiği · Orta Çağ İslam matematiği
Problemler	Apollonios problemi · Daireyi kareleştirme · Küpü iki katına çıkarma · Açıyı üçe bölme
Kavramlar/Tanımlar	Apollonius çemberi Diyofantus denklemi Çevrel çember Eşölçülebilirlik Orantılılık ilkesi Altın oran Yunan rakamları Bir üçgenin iç ve dış çemberleri Tükenme yöntemi Paralellik postülatı Platonik katılar Hipokrat ayı Hippias kuadratiksi Düzgün çokgen Cetvel ve pergelle yapılan çizimler Üçgen merkezi
Bulgular	Açıortay teoremi Dış açı teoremi Öklid algoritması Öklid teoremi Geometrik ortalama teoremi Yunan geometrik cebiri Menteşe teoremi Çevre açı teoremi Kesişme teoremi Pons asinorum Pisagor teoremi Thales teoremi Gnomon teoremi Apollonius teoremi Aristarkus eşitsizliği Crossbar (Pasch) teoremi Heron formülü İrrasyonel sayılar Menelaus teoremi Pappus'un alan teoremi Batlamyus eşitsizliği Batlamyus kirişler tablosu Batlamyus teoremi Theodorus sarmalı
Antik Yunan matematikçilerinin zaman çizelgesi