Kafes (sıra teorisi)

Kafes veya örgü, matematikte özellikle sıra kuramı ve soyut cebir alanlarında incelenen temel yapılardan biridir. Kafes, her iki elemanının hem en büyük alt sınırını (meet, ∧) hem de en küçük üst sınırını (join, ∨) belirlemenin mümkün olduğu kısmi sıralı kümeler temelinde tanımlanır. Bu yönüyle kafesler, hem sıralı yapıların hem de cebirsel işlemlerin bir araya geldiği bir çerçeve sunar.

Kafes yapıları, küme kuramından sayı teorisine, mantıksal sistemlerden bilgisayar bilimine kadar birçok farklı disiplinde doğal olarak karşımıza çıkar. Örneğin bir kümenin kuvvet kümesi, alt küme ilişkisiyle kısmi sıralanmış bir kafes oluşturur; burada birleşim işlemi join, kesişim işlemi ise meet olarak işlev görür. Benzer şekilde, doğal sayılar kümesi de bölünebilme ilişkisiyle bir kafes oluşturur; burada en küçük ortak kat join’e, en büyük ortak bölen ise meet’e karşılık gelir.

Kafesler yalnızca sıralı yapılar olarak değil, aynı zamanda iki işlemi yani birleşim (join) ve kesişim (meet) taşıyan cebirsel sistemler olarak da tanımlanabilir. Bu iki yaklaşım birbirine denktir ve kafes kuramı her iki perspektifi de birleştirir. Kafeslerin daha genel hali olan yarı-kafesler, yalnızca tek bir birleşim ya da kesişim işlemini gerektirirken; tam kafesler, bu iki işlemi birden gerektirir. Öte yandan Heyting cebirleri ve Boole cebirleri, kafeslerin mantıksal yorumlara sahip özel türleridir.

Bu bağlamda kafes kuramı, soyut cebirin bir alt dalı olarak bu yapıların özelliklerini, örneklerini ve uygulamalarını sistematik biçimde inceler.

Tanımı

Bir kafes yapısı hem bir kısmi sıralı küme olarak sıra kuramı kapsamında hem de bir cebirsel yapı olarak tanımlanabilir.

Kısmi sıralı küme olarak

Teknik olarak, kısmi sıralı bir küme $(L,\leq )$ (poset olarak kısaltılabilir) ele alındığında, eğer her iki eleman için hem en küçük ortak üst sınır (birleşim, ∨) hem de en büyük ortak alt sınır (kesişim, ∧) tanımlıysa, bu yapı bir kafes olarak adlandırılır. Yani, $L$’nin her iki elemanlı alt kümesi $\{a,b\}\subseteq L$ için bir birleşim $\vee$ (yani en küçük üst sınır, $a\vee b$ ile gösterilir) ve buna karşılık gelen bir kesişim $\wedge$ (yani en büyük alt sınır, $a\wedge b$ ile gösterilir) tanımlıdır. Örneğin, bir kümenin tüm alt kümelerinden oluşan kuvvet kümesi, alt kümeler arasındaki kapsama (dahil olma) ilişkisiyle kısmi sıralanmıştır; burada birleşim işlemi küme birleşimine, kesişim ise küme kesişimine karşılık gelir. Bu tanım, ∧ ve ∨ işlemlerini dualite prensibine uygun ikili işlemler haline getirir. Bir kafesin birleşim ve kesişim işlemleri, sıralamaya uyumlu yani monotoniktir; bu, elemanlar sıralama içinde büyürken işlemlerin de aynı yönde "büyüdüğü" anlamına gelir: Eğer $a_{1}\leq a_{2}$ ve$b_{1}\leq b_{2}$ ise, o zaman $a_{1}\vee b_{1}\leq a_{2}\vee b_{2}$ ve $a_{1}\wedge b_{1}\leq a_{2}\wedge b_{2}$ eşitsizlikleri sağlanır.

Bir tümevarım argümanıyla gösterilebilir ki, bir kafesin boş olmayan her sonlu alt kümesi, bir en küçük üst sınıra ve bir en büyük alt sınıra sahiptir. Ek varsayımlar altında daha ileri sonuçlara ulaşılabilir; bu konunun ayrıntıları için Tamlık başlığına bakılabilir. Aynı makalede, yukarıdaki tanımın, ilişkili kısmi sıralı kümeler arasında uygun Galois bağlantılarının varlığı üzerinden nasıl yeniden ifade edilebileceği de ele alınır. Bu yaklaşım, özellikle kategoriler kuramı bağlamında kafeslere yönelik çalışmalarda ve biçimsel kavram çözümlemesi alanında önem taşır.

Bir kafesin herhangi bir alt kümesi $H\subseteq L$ üzerinde birleşim ve kesişim işlemleri her zaman tanımlı olmayabilir. Bu durumda, sadece bazı durumlarda bu işlemler yapılabiliyorsa, bu yapı kısmi kafes olarak adlandırılır. Yani kısmi kafeste birleşim ve kesişim işlemleri kısmi fonksiyonlardır; her zaman sonuç kümenin içinde olmayabilir. Eğer işlemin sonucu $H$'de değilse, tanımsız kabul edilir. Kısmi kafesler, ya bir kafesin alt kümeleri olarak tanımlanabilir, ya da doğrudan belirli aksiyomları sağlayan kısmi işlemler olarak içsel biçimde ele alınabilir.

Cebirsel yapı olarak

Kafes, $(L,\vee ,\wedge )$ biçiminde tanımlanan bir cebirsel yapıdır; burada $L$ bir küme, $\vee$ ve $\wedge$ ise $L$ üzerinde tanımlı iki değişmeli ve birleşmeli işlemlerdir. Bu işlemler, tüm elemanlar $a,b\in L$ için aşağıdaki aksiyomatik özdeşlikleri sağlar (bazen “absorpsiyon kanunu” olarak adlandırılır):$$a\vee (a\wedge b)=a$$$$a\wedge (a\vee b)=a$$

Her ne kadar aşağıdaki iki eşitlik de, iki absorbsiyon kanununun birlikte alınmasıyla türetilebilir olsa bile sıklıkla aksiyom olarak kabul edilir. Bu biçimdeki özdeşlikler "etkisizlik kanunları" olarak adlandırılır. $$a\vee a=a$$ $$a\wedge a=a$$

Bu aksiyomlar, $(L,\vee )$ ve $(L,\wedge )$ yapılarını yarı-kafesler haline getirir. Yukarıdaki aksiyomlar içinde hem kesişim hem birleşimin birlikte yer aldığı tek aksiyomlar olan absorpsiyon kanunları, kafesi rastgele iki yarı-kafes çiftinden ayırır ve bu iki yarı-kafesin uygun şekilde etkileşmesini sağlar. Özellikle, her yarı-kafes diğerinin dualidir. Absorpsiyon kanunu, kesişim ve birleşim yarı-kafeslerinin aynı kısmi sıralamayı tanımlaması gerektiği şartı olarak da görülebilir.

İki tanım arasındaki bağlantı

Sıralama kuramsal bir kafes, $\vee$ ve $\wedge$ olmak üzere iki ikili işlem ortaya çıkarır. Bu işlemler için değişmeli, birleşmeli ve absorpsiyon kanunlarının kolayca doğrulanabilmesi nedeniyle, $(L,\vee ,\wedge )$ cebirsel anlamda bir kafes oluşturur.

Tersi de doğrudur. Cebirsel olarak tanımlanmış bir kafes $(L,\vee ,\wedge )$ verildiğinde, $L$ $\leq$ üzerinde kısmi bir sıralama $a,b\in L.$'nin tüm elemanları için şöyle tanımlanabilir:$$a\leq b{\text{ eğer }}a=a\wedge b,{\text{ ya da}}$$ $$a\leq b{\text{ eğer }}b=a\vee b,$$Absorpsiyon kanunları, bu iki tanımın birbirine eşdeğer olduğunu garanti eder:$$a=a\wedge b{\text{ ise }}b=b\vee (b\wedge a)=(a\wedge b)\vee b=a\vee b$$ve benzer biçimde diğer yönde de geçerlidir.

Böylece tanımlanan $\leq$ ilişkisi, orijinal $\vee$ and $\wedge$ işlemleriyle uyumlu olan bir kısmi sıralamayı ifade eder; yani bu sıralama altında ikili kesişim ve birleşim işlemleri ilk verilen $\vee$ and $\wedge$ işlemleriyle sağlanır.

Kafesin iki tanımı eşdeğer olduğundan, hangi tanımı kullanmak amaç açısından uygunsa serbestçe tercih edilebilir ve tanımların her iki yönü de kullanılabilir.

Sınırlı kafes

Bir sınırlı yani alt ve üst sınırı bulunan kafes aşağıdaki formülü sağlayan en küçük ve en büyük elemanı sırasıyla 0 (⊥) ve 1 veya (⊤) öğeleri olan bir kafes türüdür.

$$0\leq x\leq 1\;{\text{ her bir }}x\in L$$

Bir sınırlı kafes tıpkı $(L,\vee ,\wedge )$ kafesinde olduğu gibi $(L,\vee ,\wedge ,0,1)$ cebirsel form yapısında, kafesin en küçük elemanı olan $0$ birleşim işlemi $\vee$ için, en büyük elemanı olan $1$ ise kesişim işlemi $\wedge$ için etkisiz elemandır.$$a\vee 0=a$$$$a\wedge 1=a$$Kısmi sıralı kümenin bir sınırlı kafes oluşu eğer ve sadece her belirli elemanlar kümesinin (boş küme dahil) kesişim ve birleşim işlemine sahip olduğu gösterilebilir.

Her kafes, en büyük ve en küçük birer eleman eklenerek bir sınırlı kafes içine yerleştirilebilir. Ayrıca, boş olmayan her sonlu kafes zaten doğası gereği sınırlıdır; çünkü tüm elemanların birleşimi alınarak en büyük eleman ${\textstyle 1=\bigvee L=a_{1}\lor \cdots \lor a_{n}}$ ve tüm elemanların kesişimi alınarak en küçük eleman ${\textstyle 0=\bigwedge L=a_{1}\land \cdots \land a_{n}}$ elde edilir. Burada $L=\left\{a_{1},\ldots ,a_{n}\right\}$ kafesteki tüm elemanları içeren kümedir.

Diğer cebirsel yapılarla olan ilişkisi

Kafeslerin, grup benzeri cebirsel yapılar ile bazı ilişkileri bulunmaktadır. Bunun nedeni birleşim ve kesişim işlemleri hem değişmeli hem de birleşmeli olduğundan, bir kafes, aynı evrende tanımlı iki değişmeli yarıgruptan oluşan bir yapı olarak düşünülebilir. Eğer kafes sınırlıysa (yani 0 ve 1 elemanları varsa), bu yarıgruplar aslında değişmeli monoidlerdir.

Absorbsiyon yasası, yalnızca kafes teorisine özgü olan tek tanımlayıcı özelliktir. Ayrıca, bir sınırlı kafes, dağılım özelliği olmadan tanımlanmış bir değişmeli halka olarak da düşünülebilir.

Değişme, birleşme ve etkisizlik özellikleri sayesinde, birleşim ve kesişim işlemleri ikili elemanlar yerine boş olmayan sonlu kümeler üzerinde tanımlı işlemler olarak da görülebilir. Sınırlı kafeslerde boş kümenin birleşimi ve kesişimi de sırasıyla 0 ve 1 olarak tanımlıdır. Bu özellik, sınırlı kafesleri genel kafeslere kıyasla daha ‘doğal’ yapar ve bu nedenle birçok yazar, her kafesin sınırlı olmasını varsayar.

Kafeslerin cebirsel yorumu, evrensel cebir alanında temel bir rol oynar.

Örnekler

• 
  Şekil 1: $\{x,y,z\}$ kümesinin altkümeleri, küme kapsaması ilişkisine göre sıralanmıştır. "Kafes" terimi, bu yapının Hasse diyagramındaki görünümünden esinlenerek adlandırılmıştır.
• 
  Şekil  2: 60 sayısının bölenlerinden oluşan kafes, "bölme" ilişkisine göre sıralanmıştır.
• 
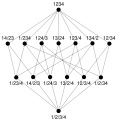
  Şekil  3: $\{1,2,3,4\}$'ün partisyonlarının kafesi, "inceltilme hali" ilişkisine göre sıralanmıştır.
• 
  Şekil  4: Pozitif tamsayıların $\,\leq$ ilişkisine göre sıralandığı kafes.
• 
  Şekil  5: Bileşenlerine göre sıralanmış negatif olmayan tam sayı çiftlerinin kafesi.

• Herhangi bir $A$ kümesi için, $A$'nın tüm altkümelerinden oluşan koleksiyon (yani $A$'nın kuvvet kümesi), alt küme kapsaması ilişkisine göre sıralandığında, boş küme ve $A$'nın kendisi tarafından sınırlandırılmış bir kafes elde edilir. Bu kafeste küme birleşimi en küçük üst sınırı, küme kesişimi ise en büyük alt sınırı verir. (Bkz. Şekil 1)
• Herhangi bir $A$ kümesi için, $A$'nın tüm sonlu alt kümelerinden oluşan ve kapsama ilişkisine göre sıralanan küme de bir kafestir. Bu kafes, $A$ yalnızca sonluysa sınırlıdır.
• Herhangi bir $A$ kümesi için, $A$'nın tüm küme bölünmesi, inceltilme hali ilişkisine göre sıralandığında bir kafes oluşturur (Bkz. Şekil 3).
• Pozitif tamsayılar, klasik ≤ sıralaması altında "min" ve "max" işlemleriyle bir sınırsız kafes oluşturur. 1 en küçük elemandır; en büyük eleman yoktur (Bkz. Şekil 4).
• Doğal sayıların Kartezyen çarpımı, $(a,b)\leq (c,d)$ olacak şekilde sıralanır; bu, $a\leq c$ ve $b\leq d$ anlamına gelir. Bu yapıda $(0,0)$ en küçük elemandır; en büyük eleman yoktur (Bkz. Şekil 5).
• Doğal sayılar ayrıca bölenlik ilişkisi altında da bir kafes oluşturur: $a\leq b$ yalnızca $a$, $b$'yi bölüyorsa geçerlidir. Bu durumda en büyük ortak bölen (GCD) en küçük üst sınır, en küçük ortak kat (LCM) ise en büyük alt sınır olur. 1 en küçük, 0 ise en büyük elemandır. Şekil 2, bu yapının sonlu bir alt kafesini gösterir.
• Her tam kafes (bununla ilgili daha fazla bilgi için aşağıdaki Tamlık bölümüne bakınız), belirli bir türde sınırlı kafestir. Bu sınıf, birçok pratik örneğe kaynaklık eder.
• Bir aritmetik tam kafesin kompakt elemanları kümesi, kafes işlemleri aritmetik kafesin işlemleriyle sınırlanmış olacak şekilde, en küçük elemana sahip bir kafes oluşturur. Bu özellik, aritmetik kafesleri yalnızca birleşim yarı-kafesi oluşturan kompakt elemanlara sahip cebirsel kafeslerden ayıran temel farktır. Bu iki kafes türü de alan kuramı içinde incelenir.

Kafes olmayan örnekler

Şekil 8: Kafes olmayan bir kısmi sıralı küme: $a$ ve $b$ öğeleri için ortak alt sınırlar $0,d,g,h$ ve $i$'dir; ancak bunlardan hiçbiri en büyük alt sınır değildir.

Şekil 7: Kafes olmayan bir kısmi sıralı küme:$b$ ve $c$ öğeleri için ortak üst sınırlar $d,e$ ve $f$'tir; ancak bunlardan hiçbiri en küçük üst sınır değildir.

Şekil 6: Kafes olmayan bir kısmi sıralı küme:$c$ ve $d$ öğelerinin hiç ortak üst sınırı yoktur.

Çoğu kısmi sıralı küme, bir kafes yapısına sahip değildir. Bunlara şu örnekler verilebilir:

• Ayrık (discrete) kısmi sıralı küme: $x\leq y$ yalnızca $x=y$ durumunda geçerliyse, bu kümeye ayrık poset denir. Böyle bir poset yalnızca bir ya da sıfır öğe içeriyorsa kafes olabilir. Örneğin, iki öğeli ayrık poset bir kafes değildir.
• Bölünebilirlik ile sıralanmış sayılar: Küme $\{1,2,3,6\}$ bölünebilirlik ilişkisiyle sıralandığında bir kafestir. Ancak $\{1,2,3\}$kümesi, aynı şekilde sıralandığında bir kafes değildir. Çünkü 2 ve 3'ün birleşimi yani en küçük ortak katları bu kümede yoktur. Benzer şekilde, $\{2,3,6\}$ kümesinde 2 ve 3'ün kesişimi yani en büyük ortak böleni bulunmamaktadır.
• Küme $\{1,2,3,12,18,36\}$: Bu küme de bölünebilirlik sırasına göre bir kafes değildir. Örneğin, 2 ve 3'ün ortak üst sınırları 12, 18 ve 36'dır. Ancak bunların hiçbiri diğerlerini bölmediği için en küçük üst sınır olamaz. Aynı şekilde, 12 ve 18'in ortak alt sınırları 1, 2 ve 3'tür, ancak bunlardan hiçbiri diğerlerini bölmediği için en büyük alt sınır olamaz.

Kafes morfizmleri

Şekil 9: Kafesler arasında tanımlanmış monoton bir fonksiyon $f$, birleşim ve kesişim işlemlerini korumamaktadır. Örneğin: $f(u)\vee f(v)=u^{\prime }\vee u^{\prime }=u^{\prime }$ $\neq$ $1^{\prime }=f(1)=f(u\vee v)$ and $f(u)\wedge f(v)=u^{\prime }\wedge u^{\prime }=u^{\prime }$ $\neq$ $0^{\prime }=f(0)=f(u\wedge v).$

Kafesler arasında bir morfizma (homomorfizma) tanımı, cebirsel tanımdan kolayca elde edilir.

İki kafes verildiğinde:$\left(L,\vee _{L},\wedge _{L}\right)$ ve $\left(M,\vee _{M},\wedge _{M}\right),$ bir kafes homomorfizması olan $f:L\to M$ fonksiyonu, $a,b\in L$ için aşağıdaki koşulları sağlamalıdır:$$f\left(a\vee _{L}b\right)=f(a)\vee _{M}f(b),{\text{ ve }}$$$$f\left(a\wedge _{L}b\right)=f(a)\wedge _{M}f(b).$$

Bu durumda $f$, her iki alt-yarı-kafesin de homomorfizması olur. Kafesler ilave yapılara sahipse (örneğin sıfır ve bir öğeleri gibi), morfizmaların bu yapıları da koruması gerekir. Özellikle, sınırlı kafesler arasında tanımlanan homomorfizmalar (genellikle doğrudan "kafes homomorfizması" denir), iki sınırlı kafes olan$L$ ve $M$ arasındaki $f$ şu koşulları da sağlamalıdır:$$f\left(0_{L}\right)=0_{M},{\text{ and }}$$$$f\left(1_{L}\right)=1_{M}.$$Kısmi sıralama bağlamında bu koşullar, fonksiyonun ikili birleşim ve kesişimi koruması anlamına gelir. Sınırlı kafesler için 0 ve 1'in korunması, boş kümenin birleşimi ve kesişiminin korunması ile eşdeğerdir. Her kafes homomorfizması, ilişkili sıralama (≤) ile uyumlu olacak şekilde monoton bir fonksiyondur. Ancak yalnızca monoton olmak yeterli değildir çünkü birleşim ve kesişimi korumayan monoton fonksiyonlar homomorfizma değildir (bkz. Şekil 9).

İzomorfizmler standart olarak tersinir morfizmalar olarak tanımlanır. Bu çerçevede bir kafes izomorfizması, sadece bire bir bir kafes homomorfizmasıdır.

Benzer şekilde:

• Bir kafes endomorfizması, bir kafesin kendisine tanımlanan bir kafes homomorfizmasıdır.
• Bir kafes otomorfizması ise, birebir örten bir kafes endomorfizmasıdır (yani, kafesin kendisine bire bir ve yapı koruyucu dönüşüm).

Kafesler ve bunların homomorfizmaları birlikte bir kategori oluşturur. Bu, kategori kuramında önemli bir yapıdır; nesneler kafeslerdir, morfizmalar ise bu kafesler arasındaki homomorfizmalardır.

Varsayalım ki:

• $\mathbb {L}$ ve $\mathbb {L} '$ iki 0 ve 1 öğelerine sahip kafeslerdir (yani sınırlı kafesler).

Bu iki kafes arasında tanımlanmış bir homomorfizma $f$:$\mathbb {L}$→$\mathbb {L} '$, “0,1-ayıran” olarak adlandırılır ancak ve ancak aşağıdaki koşullar sağlanır:

• $f^{-1}\{f(0)\}=\{0\}$ (yani yalnızca 0 öğesi 0'a gider – $f$, 0'ı ayırır)
• $f^{-1}\{f(1)\}=\{1\}$ (yani yalnızca 1 öğesi 1'e gider – $f$, 1'i ayırır)

Bu özellik, homomorfizmanın en küçük (0) ve en büyük (1) öğeleri bozmadan ve başka öğelerle karıştırmadan aktardığını ifade eder. Özellikle kafes izomorfizmalarında bu özellik otomatik olarak sağlanır çünkü izomorfizma hem yapıyı korur hem de bire birdir

Alt kafesler

Bir kafesin altkafesi, o kafesin $L$ bir altkümesidir ve bu altküme, aynı birleşim ∨ ve kesişim ∧ işlemleriyle bir kafes yapısı oluşturuyorsa, altkafes olarak adlandırılır.

Yani, eğer $L$ bir kafes ve $M$ bir altkümeyse ve her $a,b\in M$ için hem $a\wedge b$ hem de $a\vee b$ olacak şekilde işlem sonuçları yine $M$'de kalıyorsa, o zaman $M$, $L$’nin bir altkafesidir.

Bir altkafes $M$, konveks bir altkafes olarak adlandırılır ancak ve ancak şu koşulu sağlıyorsa: Her $x,y,z\in L$ ve $x,y\in M$ için eğer $x\leq z\leq y$ ise, bu durumda $z$ de $M$’nin içinde olmak zorundadır. İki eleman arasındaki tüm ara değerler de alt kafeste bulunuyorsa, bu alt kafes konveks olarak adlandırılır.

Kafeslerin özellikleri

Daha fazla bilgi: Kafes haritası

Kafeslerin ilginç özel türlerine ilişkin kimi önemli özellikler aşağıda yer almaktadır. Bunlarda ilki olan sınırlılık yukarıda izah edilmiştir.

Tamlık

Ana madde: Tam kafes

Bir kısmi sıralı küme (poset), tüm alt kümeleri için hem birleşim ∨ hem de kesişim ∧ varsa, tam bir kafes olarak adlandırılır. Bu tanım gereği, her tam kafes aynı zamanda sınırlı bir kafestir (yani hem en küçük hem de en büyük elemana sahiptir). Sınırlı kafes homomorfizmaları, genelde yalnızca sonlu birleşimleri ve kesişimleri korur. Ancak, tam kafes homomorfizmaları ise herhangi bir (sonsuz dahil) birleşimi ve kesişimi korumak zorundadır.

Herhangi bir kısmi sıralı küme, tam yarı-kafes ise, tam kafes olmak zorundadır. Bu duruma bağlı olarak, bu tür yapılarda farklı homomorfizma tanımlarıyla karşılaşılır; çünkü kısmi sıralı kümenin yapısına şu dört farklı şekilde yaklaşılabilir: Tam kafes, Tam birleşim-yarı-kafesi, Tam kesişim-yarı-kafesi, Birleşimce-tam veya kesişimce-tam bir kafes. Her yaklaşım, homomorfizmanın hangi işlemleri koruması gerektiği açısından farklılık gösterebilir.

"Kısmi kafes" terimi, "tam kafes" kavramının karşıtı değildir. Yani her tam kafes bir kafestir; her kafes bir kısmi kafestir — ancak tersi doğru değildir.

Koşullu tamlık

Ana madde: Dedekind tamlığı

Bir kafes, herhangi bir üst sınırı olan boş olmayan her altkümesinin birleşimi (en küçük üst sınırı) varsa, koşullu olarak tam (conditionally complete) kabul edilir. Bu tür kafesler, reel sayılar kümesindeki tamlık aksiyomunun doğrudan genellemesini oluşturur. Koşullu olarak tam bir kafes şu türlerden biri olabilir: Tam kafes, En büyük elemanı (1) olmayan tam kafes, En küçük elemanı (0) olmayan tam kafes ve Hem 0 hem 1 elemanından yoksun tam kafes.

Dağılırlılık

Şekil 11: En küçük modüler olmayan (dolayısıyla dağılırlık göstermeyen) kafes: N5Burada $b\leq c$ olduğu halde: * $b\vee (a\wedge c)=b$, * $(b\vee a)\wedge c=c$ olduğu için modüler yasa ihlal edilir. Aynı zamanda bu şekilde etiketlenmiş elemanlar, aşağıdaki dağılırlık denklemini de ihlal eder:$c\wedge (a\vee b)=(c\wedge a)\vee (c\wedge b),$Ancak bunun dual (çift) versiyonu sağlanır:$c\vee (a\wedge b)=(c\vee a)\wedge (c\vee b).$

Şekil 10: En küçük dağılırlık göstermeyen (ancak modüler olan) kafes M3.

Ana madde: Dağılımlı kafes

Kafesler iki ikili işlem içerdiği için, bu işlemlerden birinin diğerine göre dağılıp dağılmadığı sorusu doğar. Yani, aşağıdaki ikili yasaların tüm $a,b,c\in L$ için geçerli olup olmadığı incelenir:

∨ işleminin ∧ işlemi üzerine dağılımı:$$a\vee (b\wedge c)=(a\vee b)\wedge (a\vee c).$$∧ işleminin ∨ işlemi üzerine dağılımı:$$a\wedge (b\vee c)=(a\wedge b)\vee (a\wedge c).$$Bu iki eşitlik aslında birbirine denktir. Eğer bir kafes bu eşitliklerden birini sağlıyorsa, dağılırlık gösteren kafes olarak adlandırılır.6'dan az elemana sahip olan ve dağılırlık göstermeyen tek kafesler M₃ ve N₅ olarak bilinir. Bunlar yukarıdaki şekillerde gösterilmiştir. Bir kafes, yalnızca içinde M₃ ya da N₅’e izomorf bir alt kafes bulunmuyorsa dağılırlık gösterir. Her dağılırlık gösteren kafes, küme kafeslerine (birleşim ∨ ve kesişim ∧ işlemleriyle tanımlı) izomorftur.

Tam kafesler için daha özel dağılırlık tanımları da vardır. Bunlar örneğin:

• Frame yapıları
• Tamamen dağılırlık gösteren kafesler

gibi daha gelişmiş yapılara temel oluşturur.

Modülerlik

Ana madde: Modüler kafes

Bazı uygulamalarda dağılırlık koşulu çok katıdır. Bunun yerine daha zayıf fakat faydalı bir koşul olan modülerlik tercih edilir. Bir kafes $(L,\vee ,\wedge )$ aşağıdaki eşitlik tüm $a,b,c\in L,$ için sağlanıyorsa modüler kabul edilir:$(a\wedge c)\vee (b\wedge c)=((a\wedge c)\vee b)\wedge c.$ Bu eşitlik, şu aksiyoma da denktir: $a\leq c$⇒$a\vee (b\wedge c)=(a\vee b)\wedge c.$

Bir kafes, yalnızca içinde N₅’e izomorf bir alt kafes yoksa modülerdir. Modüler kafeslere örnekler: Bir modülün alt modül kafesi, Bir halkadaki iki taraflı idealler kafesi, Bir grubun normal alt grupları kafesi. Öte yandan, otomatik akıl yürütmede kullanılan “daha özel olma” sıralamasına dayalı terimler kümesi, modüler olmayan bir kafestir.

Yarımodülerlik

Ana madde: Yarımodüler kafes

Bir sonlu kafes, ancak ve ancak hem üstten yarı-modüler hem de alttan yarı-modüler ise modülerdir. Sonlu uzunlukta bir kafes için üstten yarı-modülerlik, kafesin dereceli (graded) olması ve derece (rank) fonksiyonu $r$’nin şu koşulu sağlaması ile eşdeğerdir:

$r(x)+r(y)\geq r(x\wedge y)+r(x\vee y).$

Dereceli kafesler için eşdeğer başka bir koşul da Birkhoff koşuludur:

Kafesteki $L,$ her $x$ ve $y$ için, eğer her ikisi de $x\wedge y$'yi kapsıyorsa, o zaman $x\vee y$ hem $x$’i hem de $y$’yi kapsar.

Bir kafes alttan yarı-modüler olarak adlandırılırsa, bu onun dualinin yarı-modüler olması anlamına gelir.

Sonlu kafesler için bu, yukarıdaki koşulların; $\vee$ ve $\wedge$ işlemlerinin yer değişmesiyle, "kapsar" işlemi yerine "tarafından kapsanır" işlemine dönüşmesiyle ve eşitsizliklerin yönünün ters çevrilmesiyle geçerli olması demektir.

Süreklilik ve cebirsellik

Alan kuramı bağlamında, bir kısmi sıralamanın öğelerini daha "basit" öğelerle yaklaşık olarak ifade etmek doğaldır. Bu durum, şu kavramları doğurur: Sürekli kısmi sıralı kümeler: Her öğe, kendisinden "çok daha küçük" öğelerden oluşan yönlü bir kümenin üst sınırı olarak ifade edilebilir. Eğer bu yönlü kümeler sadece sıkı öğelerle sınırlanırsa, poset ayrıca cebirsel olur.

Bu iki kavram kafesler için şöyle tanımlanır:

• Sürekli kafes: Tam olan ve poset olarak süreklilik gösteren kafes.
• Cebirsel kafes: Tam olan ve poset olarak cebirsel özellik gösteren kafes.

Bu kafes sınıflarının ilginç özellikleri vardır. Örneğin:

• Sürekli kafesler, belirli sonsuz-yerine-geçebilen işlemlerle tanımlanan cebirsel yapılara karşılık gelir.
• Cebirsel kafesler için benzer bir yapı tanımı bilinmemekle birlikte, bunlar Scott bilgi sistemleri ile sentaktik olarak tanımlanabilir.

Tümleyenler ve yarı tümeyenler

Ayrıca bakınız: Yarı tümleyenler

Bir kafes $L$, eğer en küçük eleman 0 ve en büyük eleman 1'e sahipse, yani sınırlı bir kafes $L$ ise, şu tanımlar geçerlidir:

İki öğe $x$ ve $y$, ancak ve ancak:$$x\vee y=1\quad {\text{ and }}\quad x\wedge y=0.$$ise birbirinin tümleyeni olur.

Ancak, her sınırlı kafeste tüm öğelerin tümleyeni olmayabilir. Bazı öğelerin hiç tümleyicisi yoktur, bazılarının ise birden fazla olabilir. Örneğin: $\{0,1/2,1\}$ kümesi (doğal sıralamasıyla) bir sınırlı kafestir, ancak ${\tfrac {1}{2}}$'nin tümleyicisi yoktur. N₅ kafesinde (Şekil 11), $a$ öğesinin iki tümleyeni vardır: $b$ ve $c$. Her öğesinin bir tümleyeni bulunan sınırlı kafeslere tümleyen kafes denir.

Hem tümleyenli hem de dağılırlık gösteren kafesler ise Boole cebiri olarak adlandırılır.

Dağılırlık gösteren bir kafeste, eğer bir öğenin $x$ tümleyeni varsa, bu tümleyen tektir.

Bu durumda şu şekilde yazılır:

• ${\textstyle \lnot x=y}$ ve denk olarak ${\textstyle \lnot y=x.}$

Bu tekil tümleyen, kafes $L$ üzerinde mantıksal olumsuzlama gibi davranan bir birli işlem tanımlar. Bu işleme tümleme denir.

Heyting cebirleri, dağılırlık gösteren ancak her öğesi için mutlaka bir tümleyen içermeyen yapılar olarak öne çıkar. Ancak her öğe $z$ için bir yarı-tümleyen vardır ve bu da ${\textstyle \lnot x}$ ile gösterilir. Yarı-tümleyici, $x\wedge y=0$ olacak şekilde, x'e göre bu koşulu sağlayan en büyük $y$'dir. Eğer bir Heyting cebirinde her yarı-tümleyici aynı zamanda gerçek bir tümleyiciyse, o cebir bir Boole cebiri olur.

Jordan–Dedekind zincir koşulu

Bir zincir', $x_{0}$'dan $x_{n}$'ye kadar olan bir öğe kümesidir: $\left\{x_{0},x_{1},\ldots ,x_{n}\right\},$ burada $x_{0}<x_{1}<x_{2}<\ldots <x_{n}.$ Bu zincirin uzunluğu, ndir; yani zincirdeki eleman sayısının bir eksiğidir.

Bir zincir, eğer her $x_{i}$, $x_{i-1}$'i kapsıyorsa —yani: $x_{i-1}<x_{i}$ arada başka hiçbir öğe yoksa her $1\leq i\leq n$ için— o zaman bu zincir maksimal zincir olarak adlandırılır.

Eğer her $x<y,$ çifti için, $x$'ten $y$'ye kadar olan tüm maksimal zincirlerin uzunluğu aynıysa, o zaman kafes Jordan–Dedekind zincir koşulunu sağlar.

Dereceli/dizili

Bir kafes $(L,\leq )$, eğer bir derece fonksiyonu ile donatılabiliyorsa dereceli, bazen de dizili olarak adlandırılır. (Ancak dizili poset teriminin farklı anlamları da olabilir.) Bu derece fonksiyonu: $r:L\to \mathbb {N}$ (veya bazen $\mathbb {Z}$) şöyle bir uyumluluk göstermelidir: Eğer $x<y$ ise, o zaman $r(x)<r(y)$. Özellikle, eğer $y$, $x$'i kapsıyorsa, yani arada başka bir öğe yoksa: $r(y)=r(x)+1.$

Bu fonksiyona derece fonksiyonu, her öğeye atadığı değere de öğenin derecesi denir.

Bir öğe $y$, bir başka öğe $x$'i kapsar, eğer:$y>x$ ise ve $y>z>x$ olacak hiçbir başka $z$ öğesi yoksa. Yani, $x\leq y$ ve $x\neq y$ olmakla birlikte, x ile y arasında başka hiçbir öğe bulunmuyorsa, y, x'i kapsıyordur $y>x$.

Serbest kafesler

Ana madde: Serbest kafes

Herhangi bir $X$ kümesi, serbest yarıkafes $FX$'i oluşturmak için kullanılabilir. Serbest yarıkafes, $X$'in tüm sonlu altkümelerinden oluşur ve yarıkafes işlemi, sıradan küme birleşimi olarak tanımlanır. Bu yapı, evrensel özelliği taşır.

Bir $X$ kümesi üzerinden tanımlı serbest kafes için, Whitman, $X$'in öğeleri üzerinden tanımlı polinomlara dayalı bir yapı önererek bir inşa yöntemi geliştirmiştir.

Kafes kuramında önemli terimler

Aşağıda, bazı önemli sıralama kuramı kavramları kafes kuramı bağlamında tanımlanmaktadır. Burada $x$, bir kafes $L$'nin bir öğesi $x$ olsun.

• Birleşime göre indirgenemez öğe (join-Irreducible); Bir öğe tüm $a,b\in L.$ için $x=a\vee b$ ve $x=a{\text{ or }}x=b$ koşullarının ikisini birden sağlıyorsa birleşime göre indirgenemez öğe olarak adlandırılır. Eğer $L$'de bir en küçük öğe $0$ varsa, bazı kaynaklar ayrıca $x\neq 0$ koşulunu sağlaması gerektiğini varsayar, bu tanımın, keyfi birleşimler için genelleştirilmiş hali $\bigvee _{i\in I}a_{i}$, tam birleşime göre indirgenemez ya da ($\lor$-indirgenemez) kavramını verir. Bu terimin duali ise, kesişime göre indirgenemez (meet-irreducible) ($\wedge$-indirgenemez) öğelerdir. Örnek olarak, şekil 2'de yer alan öğeler 2, 3, 4 ve 5 toplama göre indirgenemez; 12, 15, 20 ve 30 ise kesişime göre indirgenemezdir. Kimi tanımlarda, en küçük öğe (örneğin 1) ve en büyük öğe (örneğin 60), indirgenemez kabul edilmeyebilir. Gerçek sayılar kümesi üzerinde tanımlı sıradan kafeslerde, her öğe toplama göre indirgenemezdir ancak hiçbiri tamamen toplama göre indirgenemez değildir.
• Birleşime göre asal öğe (Join-Prime); Bir öğe $x\leq a\vee b$ ve $x\leq a{\text{ or }}x\leq b$ koşullarının ikisini birden sağlıyorsa birleşime göre asal öğe olarak adlandırılır. Yine, bazı kaynaklar $x\neq 0$ koşulunu da arar; ancak bu pek yaygın değildir. Bu da genelleştirilerek tamamen birleşime göre asal öğe kavramına ulaşılır. Bu terimin duali ise kesişime göre asal öğedir (meet-prime). Her birleşime göre asal öğe aynı zamanda birleşime göre indirgenemez öğedir. Benzer biçimde, her kesişime göre asal öğe de kesişime göre indirgenemezdir. Ancak tersine dönüş (her indirgenemez aynı zamanda asaldır) yalnızca kafes $L$ dağılımlı ise geçerlidir.

Eğer kafes $L$, bir en küçük öğe 0'a sahipse, bir öğe $x$, aşağıdaki koşulları sağlıyorsa atom olarak adlandırılır: $0<x$ ve $0<y<x$ olacak herhangi bir $y\in L$ öğesi yoktur. Bu durumda eğer $L$’nin sıfırdan farklı her öğesi için, $x\leq a$ olacak şekilde bir atom $a$ varsa, kafes atomiktir. Eğer $L$’deki her öğe, kafesin atomlarının birleşimi olarak ifade edilebiliyorsa, kafes atomistiktir.

İdeal ve onun duali olan filtre kavramları, kısmi sıralı kümelerin özel türde altkümeleri olup kafes kuramı için önemli yapılardır.

Ayrıca bakınız

• Birleşim ve kesişim (sıra teorisi) - Sıralı kümelerde birleşim (join, ∨) ve kesişim (meet, ∧) işlemleri.
• Kafesler haritası - Matematikte, farklı kafes türlerinin yapısal ilişkilerini gösteren diyagram veya şema.
• Ortokomplemanlı kafes - Her eleman için belirli kurallara uyan bir "tamamlayıcı" (kompleman) tanımlanmış olan kafes.
• Tam sıralı düzen - Her iki elemanın karşılaştırılabildiği (ya x ≤ y ya da y ≤ x olduğu) sıralı yapı
• İdeal ve filtre (ikili kavramlar) - İdeal: Boş olmayan, yukarıdan sınırlı, aşağıya kapalı alt küme. Filtre: Bunun duali, yani aşağıdan sınırlı, yukarıya kapalı alt küme.
• Eğri kafes (veya yönsüz olmayan kafes) - Birleşim ve kesişim işlemlerinin değişmeli (komütatif) olmadığı cebirsel yapı.
• Euleryen kafes - Her kapalı zincirinin tek sayı uzunluğuna sahip olduğu, belirli topolojik özellikleri taşıyan kafes.
• Post kafesi - {0,1} kümesi üzerindeki tüm klonların (bileşime kapalı ve projeksiyonları içeren işlem kümeleri) birleşim altındaki sıralaması.
• Tamari kafesi - Parantezleme biçimlerine göre sıralanmış ifadelerden oluşan matematiksel yapı.
• Young–Fibonacci kafesi - Young diyagramları ve Fibonacci sayılarına dayanan özel bir kafes yapısı.
• 0,1-basit kafes - Yalnızca en küçük (0) ve en büyük (1) elemanları olan ve belirli basitlik koşullarını sağlayan kafes.

Kafes teorisinde kullanılan uygulamalar

Birçok uygulamada kümelerin yalnızca kısmi kafesler olduğunu unutmayın: her eleman çiftinin birleşme veya birleşme noktası yoktur.

• Anlamsız topoloji
• Alt grupların kafesi
• Spektral uzay
• Değişmez alt uzay
• Kapatma operatörü
• Soyut yorumlama
• Alt tüketim kafesi
• Bulanık küme teorisi
• Birinci dereceden mantığın cebirselleştirilmesi
• Programlama dillerinin semantiği
• Alan teorisi
• Ontoloji (bilgisayar bilimi)
• Çoklu kalıtım
• Biçimsel kavram çözümlemesi ve Lattice Miner (teori ve araç)
• Bloom filtresi
• Bilgi akışı
• Sıralı optimizasyon
• Kuantum mantığı
• Medyan grafiği
• Bilgi alanı
• Düzenli dil öğrenimi
• Analojik modelleme