Dizinin limiti

Birim çemberi sınırlayan n-kenarlı düzgün çokgenlerin çevrelerinden oluşan dizinin limit değeri çemberin çevresine eşittir, yani $2\pi r$. İçine dizilmiş çokgenlere karşılık gelen dizi aynı limite sahiptir.

n	n sin(1/n)
1	0.841471
2	0.958851
...
10	0.998334
...
100	0.999983

n pozitif tam sayısı büyüdükçe, n sin(1/n) değeri 1'e yaklaşır. Bu durumda "n sin(1/n) dizisinin limiti 1'e eşittir" deriz.

Matematikte, bir dizinin limiti, dizinin terimlerinin yaklaştığı değerdir. Eğer böyle bir limit varsa diziye yakınsak denir. Yakınsamayan diziye ıraksak denir. Bir dizinin limiti, analizin nihai olarak dayandığı temel kavram olarak görülür.

Limitler, herhangi bir metrik veya topolojik uzayda tanımlanabilir. Fakat çoğunlukla gerçel sayılarda tanımlandığını görürüz.

Tarihi

Yunan filozof Zeno of Elea limit işlemleri içeren paradoksları formüle etmesiyle meşhurdur.

Leukippos, Demokritos, Antifon, Eudoksos ve Arşimet bir alan ya da bir hacmi bulmak için yaklaşımlardan oluşan ve sonsuz dizi kullanan tüketme yöntemini geliştirdi. Arşimet sonsuz dizinin terimleri toplamakta ki buna günümüzde geometrik seri diyoruz, başarılı oldu.

Newton şu eserlerinde serilerle uğraştı: Sonsuz serilerle analiz (1669'da yazıldı, el yazması olarak yayıldı, 1711'de basıldı), Diferansiyel kalkülüs ve sonsuz seriler yöntemi (1671'da yazıldı, 1736'da İngilizce çevirisi basıldı, Latince aslı ise çok sonra basıldı) ve Tractatus de Quadratura Curvarum (1693'te yazıldı, Optiks eserine ek olarak 1704'te basıldı). Sonraki eserinde, Newton (x+o)ⁿ binom açılımını ele aldı ve sonraları (o→0 kabulü ile) limit alarak doğrusallaştırdı.

18. yüzyılda, Euler gibi matematikçiler tam doğru anda durdurarak bazı ıraksak serileri toplamakta başarılı oldu; hesaplanabildiği sürece limitinin olup olmadığını umursamadılar. Yüzyılın sonunda, Lagrange, Théorie des fonctions analytiques (1797) adlı eserinde titizlik eksikliğinin kalkülüste daha fazla ilerlemenin önüne geçtiğini söyledi. Gauss, hipergeometrik seriler (1813) adlı çalışmasında bir serinin hangi şartlar altında bir limite yakınsadığını ilk kez titizlikle inceledi.

Limitin modern tanımı (her ε için öyle bir N indisi vardır ki ...) Bernhard Bolzano (Der binomische Lehrsatz, Prag 1816, o zamanlar çok az dikkat çekti) ve 1870'lerde Karl Weierstrass tarafından yapıldı.

Gerçel sayılar

{a_n} yakınsak dizisinin grafiği mavi ile gösteriliyor. n artarken dizinin 0 limit değerine yakınsadığı görülebiliyor.

Gerçel sayılarda, eğer dizideki sayılar başka bir sayıya değil de yalnızca $L$'ye yaklaşıyorsa $L$ sayısı $(x_{n})$ dizisinin limitidir.

Örnekler

• Eğer bir c sabiti için $x_{n}=c$ ise, $x_{n}\to c$.
• Eğer $x_{n}=1/n$ ise, $x_{n}\to 0$.
• Eğer $n$ çift iken $x_{n}=1/n$ ise ve $n$ tek iken $x_{n}=1/n^{2}$ ise, $x_{n}\to 0$. ($n$ tek iken $x_{n+1}>x_{n}$ olması konuyla alakasızdır.)
• Herhangi bir gerçel sayı için, ondalık yaklaşmalar yapılarak o sayıya yakınsayan bir dizi oluşturabilir. Örneğin, $0.3,0.33,0.333,0.3333,...$ dizisi $1/3$ sayısına yakınsar. Dikkat edilmeli ki $0.3333...$ ondalık gösterimi az önceki dizinin limitidir ve matematiksel olarak şöyle tanımlanır

$0.3333...\triangleq \lim _{n\to \infty }\sum _{i=1}^{n}{\frac {3}{10^{i}}}$.

• Bir dizinin limitini bulmak her zaman kolay değildir. Örneğin, $\lim _{n\to \infty }\left(1+{\frac {1}{n}}\right)^{n}$, aynı zamanda e sayısı olarak bilinir veya Aritmetik-geometrik ortalama. Bu gibi durumlarda sıkıştırma teoremi genellikle kullanışlıdır.

Biçimsel Tanım

Aşağıdaki şart sağlanıyorsa "$(x_{n})$ dizisinin limiti $x$ sayısıdır" deriz:

• Her $\epsilon >0$ gerçel sayısı için, öyle bir $N$ doğal sayısı vardır ki, her $n>N$ doğal sayısı için, $|x_{n}-x|<\epsilon$ elde ederiz.

Başka bir ifade ile, her $\epsilon$ yakınlık ölçüsü için, dizinin terimleri o miktarda limite yakındır. $(x_{n})$ dizisi $x$ limitine yakınsıyor ya da yaklaşıyor denilir ve $x_{n}\to x$ veya $\lim _{n\to \infty }x_{n}=x$ biçiminde yazılır.

Eğer dizi bir limite yakınsıyorsa, o zaman yakınsaktır, aksi takdirde ıraksaktır.

Özellikler

Dizilerin limitleri sıradan aritmetik işlemlere benzer davranır. Eğer $a_{n}\to a$ ve $b_{n}\to b$ ise, $a_{n}+b_{n}\to a+b$ ve $a_{n}b_{n}\to ab$. b ve $b_{n}$ sıfırdan farklı ise, $a_{n}/b_{n}\to a/b$.

Herhangi bir f sürekli fonksiyonu için, $x_{n}\to x$ ise, $f(x_{n})\to f(x)$. Aslında, herhangi bir gerçel değerli f fonksiyonu sürekli ise ancak ve ancak dizilerin limitlerini değiştirmiyordur. (Ama süreklilik daha genel bir kavram olarak ele alındığında bunun doğru olması gerekmez.)

Gerçel dizilerin limitlerinin diğer bazı önemli özellikleri şunlardır:

• Bir dizinin limiti biriciktir.
• $\lim _{n\to \infty }(a_{n}\pm b_{n})=\lim _{n\to \infty }a_{n}\pm \lim _{n\to \infty }b_{n}$
• $\lim _{n\to \infty }ca_{n}=c\lim _{n\to \infty }a_{n}$
• $\lim _{n\to \infty }(a_{n}b_{n})=(\lim _{n\to \infty }a_{n})(\lim _{n\to \infty }b_{n})$
• $\lim _{n\to \infty }{\frac {a_{n}}{b_{n}}}={\frac {\lim _{n\to \infty }a_{n}}{\lim _{n\to \infty }b_{n}}}$ (Eğer $\lim _{n\to \infty }b_{n}\neq 0$ ise)
• $\lim _{n\to \infty }a_{n}^{p}=\left[\lim _{n\to \infty }a_{n}\right]^{p}$
• Bazı $N$lerden daha büyük tüm $n$ler için $a_{n}\leq b_{n}$ ise, $\lim _{n\to \infty }a_{n}\leq \lim _{n\to \infty }b_{n}$.
• (Sıkıştırma Teoremi) Tüm $n>N$ için $a_{n}\leq c_{n}\leq b_{n}$ ve $\lim _{n\to \infty }a_{n}=\lim _{n\to \infty }b_{n}=L$ ise, $\lim _{n\to \infty }c_{n}=L$.
• Eğer bir dizi sınırlandırılmış ve monotonik ise o dizi yakınsaktır.
• Bir dizi yakınsak ise ancak ve ancak tüm alt dizileri de yakınsaktır.

Bu özellikler hantal resmi tanımların doğrudan kullanımına gerek kalmaksızın limitleri kanıtlamak için yaygın olarak kullanılır. Yukarıdaki özellikleri kullanarak bir kere $1/n\to 0$ olduğu ispatlandıktan sonra ${\frac {a}{b+c/n}}\to {\frac {a}{b}}$, ($b\neq 0$) olduğunu göstermek kolaydır.

Sonsuz limitler

Her K için, bir N vardır öyle ki, her $n\geq N$ için, $x_{n}>K$; öyle ki seçilen herhangi K için dizinin terimleri o K değerinden daha büyük ise, $(x_{n})$ dizisi sonsuza yaklaşıyor denilir ve $x_{n}\to \infty$ veya $\lim _{n\to \infty }x_{n}=\infty$ şeklinde ifade edilir. Benzer bir şekilde, her K için, bir N vardır öyle ki, her $n\geq N$ için, $x_{n}<K$ ise $x_{n}\to -\infty$. Eğer bir dizi sonsuza ya da eksi sonsuza yaklaşıyorsa, o dizi ıraksaktır. (Ancak, ıraksak bir dizi sonsuza ya da eksi sonsuza yaklaşmak zorunda değildir.)

Metrik uzaylar

Tanım

Tüm ε > 0 için, bir N vardır öyle ki, her $n\geq N$ için, $d(x_{n},x)<\epsilon$ ise (X, d) metrik uzayının bir x noktası (x_n) dizisinin limitidir. Bu tanım $X=\mathbb {R}$ ve $d(x,y)=|x-y|$ iken gerçel sayılar için yapılmış tanım ile aynıdır.

Özellikler

Herhangi bir f sürekli fonksiyonu için, eğer $x_{n}\to x$ ise, $f(x_{n})\to f(x)$. Aslında, bir f fonksiyonu sürekli ise ancak ve ancak uygulandığında dizilerin limitlerini değiştirmiyordur.

Eğer varsa dizilerin limitleri biriciktir, farklı noktaların belli bir pozitif uzaklık ile ayrılması gibi, bu uzaklığın yarısından az her $\epsilon$ için, dizinin terimleri her iki noktadan $\epsilon$ uzaklığı içerisinde olamaz.

Topolojik uzaylar

Tanım

x'in her U komşuluğu için, bir N vardır öyle ki, her $n\geq N$, $x_{n}\in U$ ise (X, τ) topolojik uzayında bir x noktası, (x_n) dizisinin limitidir. Eğer (X,d) metrik uzay ve $\tau$ d tarafından üretilen bir topoloji ise bu tanım metrik uzay için yapılmış tanım ile aynıdır.

Bir T topolojik uzayında $\left(x_{n}:n\in \mathbb {N} \right)\;$ noktalarının bir dizisinin limiti, özel bir fonksiyonun limitidir: bu fonksiyonun; tanım kümesi, $\mathbb {N} \cup \lbrace +\infty \rbrace$ ile genişletilmiş gerçel sayılar kümesinin indüklenmiş topoloji uzayındaki $\mathbb {N}$ kümesidir, değer kümesi T, girdisi n - bu uzayda $\mathbb {N}$'nın limit noktası olan - +∞'a yaklaşır.

Özellikler

Eğer X Hausdorff uzayı ise, dizilerin limitleri var oldukları yerde biriciklerdir. Bunun genel bir durum olması gerekmediğine dikkat edin. Özellikle, x ve y noktaları topolojik olarak benzer ise, x değerine yakınsayan herhangi bir dizi y değerine de yakınsamalıdır. Bunun tersi de geçerlidir.

Cauchy dizileri

Ana madde: Cauchy dizisi

x_n ve n eksenlerinde bir (x_n) Cauchy dizisinin grafiği mavi ile gösteriliyor. Dizideki terimler birbirine gitgide yaklaştıkça ve n değeri büyüdükçe dizinin bir limit noktasına yakınsadığını görsel olarak görebiliyoruz. Gerçel sayılarda her Cauchy dizisi bir limite yakınsar.

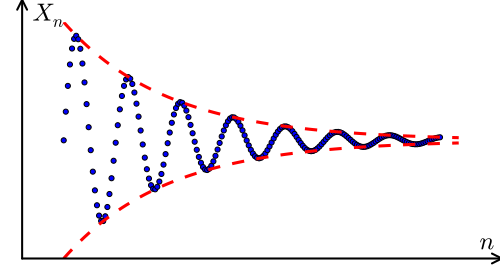
Cauchy dizisi, n değeri büyüdükçe terimleri birbirine çok çok yakınlaşan bir dizidir. Cauchy dizisi kavramı, metrik uzayda diziler ve özellikle gerçel analiz çalışmalarında çok önemlidir. Gerçel analizin en önemli sonuçlarından biri Diziler için yakınsaklığın Cauchy krakterizasyonudur.

Bir dizi yakınsaksa ancak ve ancak Cauchy'dir.

Hiperreel sayılarda tanımı

Hiperreel sayılar kullanılarak yapılan limit tanımı "indisin çok büyük değerlerine karşılık gelen terim limite çok yakın olur" sezgisini formüle eder. Daha net olursak, eğer bütün sonsuz hipernatürel H için, x_H terimi L sayısına sonsuz yakındır, yani, x_H - L farkı sonsuz küçüktür. Buna eşit olarak, L x_H'ın standard parçasıdır

$L={\rm {st}}(x_{H})\,$.

Nitekim, limit şu formül ile tanımlanabilir

$\lim _{n\to \infty }x_{n}={\rm {st}}(x_{H}),$

ki limit varsa ancak ve ancak eşitliğin sağ tarafı sonsuz bir H seçiminden bağımsızdır.

Ayrıca bakınız

• Fonksiyonun limiti
• Netin Limitii — Net bir dizinin topolojik genellemesidir.
• Yakınsaklık modları
• Kayma kuralı

Kaynakça

• Courant, Richard (1961). "Differential and Integral Calculus Volume I", Blackie & Son, Ltd., Glasgow.
• Frank Morley and James Harkness A treatise on the theory of functions (New York: Macmillan, 1893)
• Vikipedi Limit of a sequence maddesi. (Son Erişim Tarihi: 02.08.2015)

Dış bağlantılar

• Hazewinkel, Michiel, (Ed.) (2001), "Limit", Encyclopaedia of Mathematics, Kluwer Academic Publishers, ISBN 978-1556080104  (İngilizce)
• A history of the calculus (İngilizce)