Yönlü çizge
Görünüm
| Makale serilerinden |
| Ağ bilimi |
|---|
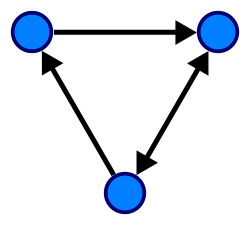
Çizge teorisinde, yönlü çizge düğümler ve hepsi birer yöne sahip kenarlardan oluşan çizgedir.
Tanım
[değiştir | kaynağı değiştir]Biçimsel terimlerle, bir yönlü çizge G = (V,A) sıralı çiftiyle ifade edilir:[1]
- V düğümler ya da noktalar kümesidir,
- A sıralı düğüm çiftlerinden oluşur ve oklar' ya da yönlü kenarlar kümesi olarak adlandırılır.
Yönlü çizge, kenarları sırasız düğüm çiftlerinden oluşan yönsüz çizgelerden ayrılır.
Yukarıdaki tanıma binaen aynı kaynaktan aynı hedefe giden birden fazla ok olamaz, ancak bazı yazarlar çok oklu daha geniş bir tanımı benimser; bu durumda tanım kümeyle değil çoklukümeyle yapılır. Yine yukarıdaki tanıma binaen, yönlü çizgeler döngülere sahip olabilir (çıktığı düğüme dönen oklar), ancak bazı yazarlar buna izin vermeyen daha dar bir tanımı benimser.[2] Özel olarak, döngüsel oklara sahip olmayan yönlü çizgeler basit yönlü çizge olarak adlandırılır.
Ayrıca bakınız
[değiştir | kaynağı değiştir]Kaynakça
[değiştir | kaynağı değiştir]- ^ Bang-Jensen & Gutin (2000). Diestel (2005), Kısım 1.10. Bondy & Murty (1976), Kısım 10.
- ^ Chartrand, Gary (1977). Introductory Graph Theory. Courier Corporation. ISBN 9780486247755. 28 Aralık 2019 tarihinde kaynağından arşivlendi. Erişim tarihi: 10 Nisan 2020.
Konuyla ilgili yayınlar
[değiştir | kaynağı değiştir]- Bondy, John Adrian; Murty, U. S. R. (1976), Graph Theory with Applications, North-Holland, ISBN 0-444-19451-7.
- Diestel, Reinhard (2005), Graph Theory, 3, Springer, ISBN 3-540-26182-6, 28 Temmuz 2011 tarihinde kaynağından arşivlendi15 Ekim 2020
- Harary, Frank; Norman, Robert Z.; Cartwright, Dorwin (1965), Structural Models: An Introduction to the Theory of Directed Graphs, New York: Wiley.
- n düğümlü yönlü çizgelerin sayısı 18 Ekim 2020 tarihinde Wayback Machine sitesinde arşivlendi. On-Line Encyclopedia of Integer Sequences

