Planck sabiti

"Planck formülü" buraya yönlendirilmektedir. Kara cisim ışınımı için Planck kanunu sayfasına bakınız.

h değerleri	Birimler
6,62606957(29)×10-34	J·s
4,135667516(91)×10-15	eV·s
6,62606957(29)×10-27	erg·s
ħ değerleri	Birimler
1,054571726(47)×10-34	J·s
6,58211928(15)×10-16	eV·s
1,054571726(47)×10-27	erg·s
hc değerleri	Birimler
1,98644568×10-25	J·m
1,23984193	eV·μm

Planck sabiti (h), bir fizik sabitidir ve kuantum mekaniğindeki aksiyonum kuantumu için kullanılır. Değeri h= 6.62607015×10−34 J⋅s' dir. Planck sabiti daha önceleri bir Fotonun enerjisi (E) ile elektromanyetik dalgasının frekansı (ν) arasında bir orantı idi. Enerji ile frekans arasındaki bu ilişki Planck ilişkisi veya Planck formülü olarak adlandırılır:

$E=h\nu \,.$

$\nu$, frekans; λ, dalga boyu ve c ışık hızı olduğunda aralarında λν = c ilişkisi vardır. Planck formülü şöyle de ifade edilebilir:

$E={\frac {hc}{\lambda }}.\,$

Bir parçacığın çizgisel momentumu p ise, parçacığın λ olasılık dalgası şöyle olur:

$\lambda ={\frac {h}{p}}.$

Frekans, çevrim bölü saniye yerine radyan bölü saniye açısal frekansı olarak ifade edilirse, Planck sabiti içindeki 2π katsayısı yutulur. Bu durumda sabit, indirgenmiş Planck sabiti veya Dirac sabiti adını alır. Bu, Planck sabitinin 2π'ye bölümüne eşittir ve ħ ("h-çubuk") sembolü ile gösterilir:

$\hbar ={\frac {h}{2\pi }}.$

Bir fotonun enerjisi ω açısal frekansına bağlı olarak şöyledir.

$E=\hbar \omega .$

Burada, ω = 2πν 'dir. İndirgenmiş Planck sabiti, kuantum mekaniğinde açısal momentumun kuantumudur.

Planck sabiti, kuantum kuramını bulanlardan biri olan, Max Planck'tan sonra adlandırıldı. Sabit 1900'de keşfedildi. Klasik istatistiksel mekanikte h ın değeri değel kendisinin olması gerekir.

Değeri

Planck sabiti, kuantum mekaniğinde aksiyonun temel birimi (kuantumu) olarak düşünülebilecek bir sabittir. Birimi SI'da joule-saniye (J·s) veya (N·m·s).

Planck sabitinin değeri;

$h=6.626\ 069\ 57(29)\times 10^{-34}\ \mathrm {J\cdot s} =4,135\ 667\ 516(91)\times 10^{-15}\ \mathrm {eV\cdot s} .$

İndirgenmiş planck sabitinin değeri;

$\hbar ={{h} \over {2\pi }}=1,054\ 571\ 726(47)\times 10^{-34}\ \mathrm {J\cdot s} =6,582\ 119\ 28(15)\times 10^{-16}\ \mathrm {eV\cdot s} .$

Parantezler arasındaki iki rakam (örneğin 29 sayısı), yaklaşık değerin standart hatasını ifade eder.

Kökenleri

Kara cisim ışınımı

Ana madde: Planck kanunu

Bir kara delik tarafından yutulan herhangi bir frekanstaki ışık şiddeti. Her bir renk, farklı sıcaklığı ifade eder. Bu eğrilerin şekillerini ilk açıklayan Planck idi.

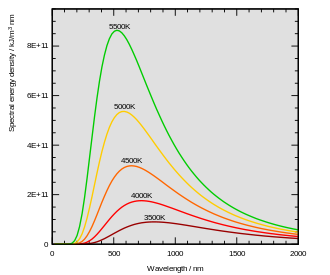
19. yüzyılda Planck, kara cisim ışınımı problemini ilk inceleyen kişi idi. Fakat bunu Kirchhoff 40 yıl önce ortaya çıkarmıştı.

Fotoelektrik etki

Ana madde: Fotoelektrik etki

Işığın madde yüzeyine düşmesi sonucu maddeden elektron yayılması olayıdır. İlk kez 1839'da Alexandre Edmond Becquerel tarafından gözlemlendi. Fakat genellikle Heinrich Rudolf Hertz'e ithaf edilir. Hertz ilk kez eksiksiz olarak 1887'de yayımlamıştır.

Atomik yapı

Ana madde: Bohr modeli

Hidrojen atomunun Bohr modelinin şeması. n=3 yörüngesinden n=2 yörüngesine doğru bir hal değişimi görülüyor. Burada görünür ışığın dalga boyu artarak 656 nm (kırmızı) olur.

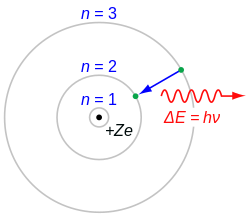
Niels Bohr, atom yapısını ilk belirleyen (1913'te) Danimarkalı fizikçidir. Bohr atomundaki bir elektron belirli miktarda enerjiye sahiptir ve E_n enerjisi şu formülle bulunur:

$E_{n}=-{\frac {hc_{0}R_{\infty }}{n^{2}}}$

Burada R_∞, üstel tanımlı sabit (Rydberg sabiti) ve n, herhangi bir tam sayı (n = 1, 2, 3, ...). Elektron en düşük enerji yörüngesine ulaştıktan sonra n = 1), artık çekirdeğe daha fazla yaklaşamaz (düşük enerji). Bu yaklaşımdan yola çıkarak Bohr Rydberg formülünü hesapladı.

Parçacığın enerjisi ve hc ifadesi

Frekansı ν olan bir fotonun enerjisi $E=h\nu =\hbar \omega$ formülüyle hesaplanabilir. Fotonun hızı c olduğu için frekansı $\nu ={\frac {c}{\lambda }}$ şeklinde yazılabilir. Bu sayede enerji ifadesi:

$E={\frac {hc}{\lambda }}$ haline dönüşür. Böylece dalga boyu bilinen bir ışığın enerjisinin hızlıca hesaplanabilmesi için hc ifadesinin hesaplanmış büyüklüğü,

$hc=1239{\mbox{eV}}{\mbox{nm}}\,$ veya

$hc=1974\cdot 10^{-19}{\mbox{J}}{\mbox{nm}}$ kullanılır.

Örnek

Kırmızı ışık ortalama 682,5 nanometre dalga boyuna sahiptir. Buna göre; $E={\frac {1239{\mbox{eV}}{\mbox{nm}}}{682,5{\mbox{nm}}}}=1,8{\mbox{eV}}$ bir fotonun enerjisi olarak bulunur.

Turuncu ışık ortalama 607,5 nanometre dalga boyuna sahiptir. Buna göre; $E={\frac {1239{\mbox{eV}}{\mbox{nm}}}{607.5{\mbox{nm}}}}=2,0{\mbox{eV}}$ bir fotonun enerjisi olarak bulunur.

Sarı ışık ortalama 577,5 nanometre dalga boyuna sahiptir. Buna göre; $E={\frac {1239{\mbox{eV}}{\mbox{nm}}}{577.5{\mbox{nm}}}}=2,1{\mbox{eV}}$ bir fotonun enerjisi olarak bulunur.

Yeşil ışık ortalama 532,5 nanometre dalga boyuna sahiptir. Buna göre; $E={\frac {1239{\mbox{eV}}{\mbox{nm}}}{532.5{\mbox{nm}}}}=2,3{\mbox{eV}}$ bir fotonun enerjisi olarak bulunur.

Mavi ışık ortalama 467,5 nanometre dalga boyuna sahiptir. Buna göre; $E={\frac {1239{\mbox{eV}}{\mbox{nm}}}{467.5{\mbox{nm}}}}=2,6{\mbox{eV}}$ bir fotonun enerjisi olarak bulunur.

Mor ışık ortalama 410 nanometre dalga boyuna sahiptir. Buna göre; $E={\frac {1239{\mbox{eV}}{\mbox{nm}}}{410.5{\mbox{nm}}}}=3{\mbox{eV}}$ bir fotonun enerjisi olarak bulunur.

Kuantum mekaniği

Ana madde: Kuantum mekaniği

Planck sabiti kuantum mekaniğinde etki edilen en küçük birimi temsil eder, diğer bir deyişle süreksizliğin birimidir. Kuantum mekaniğinde açısal momentumun x, y ve z bileşen operatörlerinin komutatörleri döndürme grubu $SO_{3}$ ve ona homomorfik olan $SU_{2}$ gruplarının Lie cebrini sağlar. Planck sabitinin en küçük etki birimi olduğu buradan da görülebilir.

$[L_{x},L_{y}]=i\hbar L_{z}$

$[L_{y},L_{z}]=i\hbar L_{x}$

$[L_{z},L_{x}]=i\hbar L_{y}$

en genelinden $e_{ijk}\,$ permütasyon sembolü olmak üzere

$[L_{i},L_{j}]=e_{ijk}i\hbar L_{k}$ ' dir.

Ayrıca bakınız

• Doğal birimler
• Planck birimleri