Kesin dışbükey uzay

Ortadaki birim yuvar kesin dışbükeyken diğer ikisi, birim küreleri üzerinde bir doğru paraçası taşıdıkları için kesin dışbükey değildir.

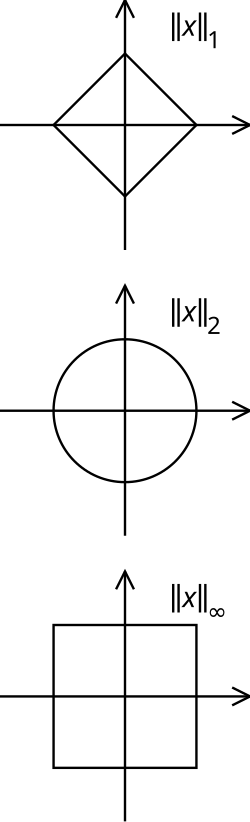
Matematikte kesin dışbükey uzay kapalı birim yuvarı kesin dışbükey küme olan normlu vektör uzaylarına verilen addır. Daha sezgisel bir biçimde ifade etmek gerekirse, birim küresi üzerinde birbirinden farklı x vey noktaları alınan bir (X, ||.||) uzayının kesin dışbükey olması için bu noktaları birleştiren doğru parçasının birim küreyi sadece x ve y noktalarında kesmesi gerekmektedir.

Kesin dışbükeylik, yapı açısından, bir iç çarpım uzayı (tüm iç çarpım uzayları kesinlikle dışbükey olduğundan) ile genel bir normlu uzay arasında bir yerdedir. Ayrıca, $X$'teki bir elemanın, bir $Y$ dışbükey altuzayindaki elemanlar üzerinden en iyi yaklaşıklamasının biricikliğini, böyle bir yaklaşıklıklama varsa, garanti etmektedir.

Normlu bir uzay tam ise ve biraz daha güçlü bir özellik olan düzgün dışbükeyliliği (ki bu da kesin dışbükeyliği verir) sağlıyorsa, o zaman Milman-Pettis teoremine göre yansımalı uzaydır.

Özellikler

Aşağıdaki özellikler kesin dışbükeyliğe eşdeğerdir.

• Normlu bir vektör uzayı (X, || ||)'in kesin dışbükey olması için gerekli ve yeterli şart x ≠ y ve || x || = || y || = 1 için || x + y || < 2 eşitsizliğinin sağlanmasıdır.
• Normlu bir vektör uzayı (X, || ||)'in kesin dışbükey olması için gerekli ve yeterli şart x ≠ y ve || x || = || y || = 1 için || αx + (1 − α)y || < 1 eşitsizliğinin 0 < α < 1 olmak üzere sağlanmasıdır.
• Normlu bir vektör uzayı (X, || ||)'in kesin dışbükey olması için gerekli ve yeterli şart x ≠ 0, y ≠ 0 ve || x + y || = || x || + || y || için x = cy eşitliğinin bir c > 0 tarafından sağlanmasıdır.
• Normlu bir vektör uzayı (X, || ||)'in kesin dışbükey olması için gerekli ve yeterli şart (X, || ||) uzayının dışbükeylik modülü δ için δ(2) = 1 olmasıdır.

Ayrıca bakınız

• Düzgün dışbükey uzay
• Dışbükeylik modülü
• Düzgün pürüzsüz uzay