Fermi-Dirac istatistikleri

Fermi-Dirac istatistikleri (F-D istatistikleri), fizik biliminin bir parçası olarak Pauli dışlama prensibine uyan eş parçacıkları içeren sistemdeki bir parçacığın enerjisini tanımlar. Birbirlerinden bağımsız olarak bunu keşfeden Enrico Fermi ve Paul Dirac'tan sonra adlandırılmıştır.

F-D istatistikleri termal dengedeki sistemdeki yarım tam sayı spine sahip eş parçacıklara uygulanır. Ek olarak, sistemdeki parçacıklarının göz ardı edilebilir karşılıklı etkileşimlerin olduğu kabul edilmektedir. Bu çok parçacıklı bir sistemin tek tek parçacıkların enerji seviyesi ile tanımlanmasına imkân kılar. Sonuç Fermi-Dirac parçacıklarının bu enerji seviyeleri üzerine dağılımını ve sistemin özelliklerini oldukça etkileyen iki farklı parçacığın aynı seviyeye sahip olmasını içerir. Fermi-Dirac istatistikleri yarım tam sayı spinli parçacıklara uygulanabildiğinden bu parçacıklar fermiyon olarak adlandırılır. En genel olarak 1/2 spine sahip fermiyon olan elektrona uygulanır. Fermi-Dirac istatistikleri, mekanik ilkelerini kullanarak daha genel bir alan olan istatistiksel mekanik alanının içerisindedir.

Tarihçe

1926'da Fermi-Dirac istatistikleri bulunmadan önce elektronun davranışların çelişkili fenomenlerden dolayı tahmin etmek güçtü. Örneğin, oda sıcaklığındaki metallerin elektronik kapasitesi elektrik akımındakinden 100 kat daha az elektronmuş gibi gözüküyordu. Ayrıca oda sıcaklığında metallere güçlü elektrik alan uygulayarak elde edilen emisyon akımının neredeyse sıcaklıktan bağımsız olması çok anlaşır bir durum değildi.

O zamanlar metallerin elektron teorisindeki zorluklarının temel sebebi elektronların(klasik istatistiğe göre)hepsinin denk olmasıdır. Başka bir deyişle her bir elektrona Boltzmann sabiti k ile orantılı olarak eşit miktarda ısı dağıldığını kabul ediliyordu.Bu istatistiksel problem F-D istatistikleri bulunana kadar çözümsüz kaldı.

F-D istatistiklerini ilk olarak 1926'da Enrico Fermi ve Paul Dirac tarafından yayınlandı.Başka bir kaynağa göre ise ilk olarak 1925'te Pascual Jordan tarafından aynı istatistiğin geliştirilerek ''Pauli'' istatistiği olarak adlandırıldığını belirtir. Ancak Dirac'a göre ilk olarak Fermi tarafından çalışıldığını ve Dirac'ın Fermi istatistikleri olarak adlandırıp karşılık gelen parçacıklara fermiyon adı verdiği bilinir.

F-D istatistikleri 1926'da Fowler bir yıldızın bir beyaz cüceye çarpışını açıklarken uygulamıştır.1927'de Sommerfeld bunu metaldeki elektronlara uygulamış ve 1928'de Fowler ve Nordheim metallerin alan elektron emisyonuna uygulamışlardır.

Fermi-Dirac dağılımı

Eş fermiyonlardan oluşan bir sistemdeki tek-parçacık seviyesi i 'deki ortalama fermiyum sayısı Fermi-Dirac dağılımı ile belirlenir.

{\bar {n}}_{i}={\frac {1}{e^{(\epsilon _{i}-\mu )/kT}+1}}

k Boltzmann sabiti, T mutlak sıcaklık, $\epsilon _{i}\$ tek-parçacık seviyesi $i$ 'nin enerjisi ve $\mu \$ kimyasal potansiyeldir.T=0 olduğunda kimyasal potansiyel, Fermi enerjisine eşittir. Yarıiletkenlerdeki electronlarda $\mu \$ de Fermi derecesi olarak adlandırılır.

F-D dağılımı sistemdeki fermiyon sayısı çok yüksek olduğunda geçerlidir, bu sebepten sisteme eklenen bir fermiyonun $\mu \$ 'ye olan etkisi göz ardı edilebilir.F-D dağılımı Pauli dışlama prensibi kullanılarak oluşturulduğundan bunun sonucu olarak $0<{\bar {n}}_{i}<1$ .

Fermi–Dirac dağılımı
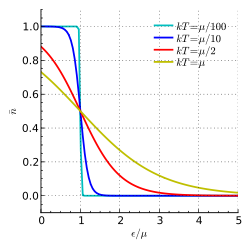
Enerji bağımlılığı. Yüksek T 'de daha kademeli. ${\bar {n}}$ = 0.5 $\epsilon \;$ = $\mu \;$ . olduğunda. $\mu \$ 'da azalma düşük T değerlerinde görülmemektedir.
Sıcaklık bağımlılığı $\epsilon >\mu \$ için.

(Büyütmek için resimlerin üzerine tıklayınız.)

Enerjiye göre parçacıkların dağılımı

Yukarıdaki dağılım, aynı anda aynı seviyeye iki farklı fermiyum sahip olamayacağından eş fermiyumların tek-parçacık enerji seviyelerine göre dağılımını göstermektedir-D dağılımı kullanılarak aynı enerjiye sahip birden fazla fermiyumun olduğu enerjiye göre bir dağılım da bulanabilir. Seviyelere göre değil de enerjiye göre yapılan bu dağılımda bazen F-D dağılımı olarak adlandırılır, ancak bu makale de bu adlandırma ile o kastedilmemektedir.

 $\epsilon _{i}\$  enerjisine sahip Ortalama fermiyon sayısı   ${\bar {n}}_{i}\$ 'nin  degeneracy   $g_{i}\$  ile çarpılması ile bulunur(örneğin  $\epsilon _{i}\$  enerjisine sahip olan seviye),

Eq. (1)'deki, $n(\epsilon )\,$ and $n_{s}\,$ sırasıyla ${\bar {n}}_{i}$ and ${\bar {n}}(\epsilon _{i})$ bu makalede tekâmül eder.

{\begin{alignedat}{2}{\bar {n}}(\epsilon _{i})&=g_{i}\ {\bar {n}}_{i}\\&={\frac {g_{i}}{e^{(\epsilon _{i}-\mu )/kT}+1}}\\\end{alignedat}}

$g_{i}\geq 2\$ olduğunda, $\ {\bar {n}}(\epsilon _{i})>1$ mümkündür, $\epsilon _{i}\$ enerjiye sahip fermiyon birden fazla seviyeye sahip olabilir.

Sürekli gibi olan $\epsilon \$ enerji seviye yoğunluğu $g(\epsilon )\$ ile değiştirildiğinde (şöyle ki birim enerji aralığında birim hacimdeki seviye sayısı), birim enerji aralığında birim hacimdeki ortalama fermiyon sayısı:

{\bar {\mathcal {N}}}(\epsilon )=g(\epsilon )\ F(\epsilon )

$F(\epsilon )\$ Fermi fonksiyonu olarak bilinir ve ${\bar {n}}_{i}$ F-D dağılımı için kullanılan fonksiyon ile aynıdır.

F(\epsilon )={\frac {1}{e^{(\epsilon -\mu )/kT}+1}}

böylece

{\bar {\mathcal {N}}}(\epsilon )={\frac {g(\epsilon )}{e^{(\epsilon -\mu )/kT}+1}}

.

Kuantum ve klasik rejimler

Maxwell-Boltzmann (MB) istatistikleri'in F-D istatistiklerine yakınsama olarak kullanılabileceği klasik rejimde parçacığın konum ve momentum için Heisenberg belirsizlik ilkesinin limitlerine yaklaşmayan durumları ele alır. Bu yaklaşımda, parçacığın ortalama de Broglie dalgaboyu ${\bar {\lambda }}$ dan çok daha büyük, ortalama ara parçacık ayrımı ${\bar {R}}$ denk gelen parçacığın konsantrasyonuna sahip olduğu durumlarda klasik durumun olduğu gösterilebilir.

{\bar {R}}\ \gg \ {\bar {\lambda }}\ \approx \ {\frac {h}{\sqrt {3mkT}}}

$h$ Planck sabiti ve $m$ parçacığın kütlesidir. T=300K'de (ortalama olarak oda sıcaklığı)tipik bir metale elektron yüklemede sistem klasik rejimden oldukça uzaktadır, çünkü ${\bar {R}}\approx {\bar {\lambda }}/25$ .Bu durum elektronun küçük kütlesi ve metale yüklenen elektronların konsantrasyonun yüksek olmasından kaynaklanır. Bu durum tipik bir metale elektron yüklemede F-D istatistiklerine ihtiyaç doğurur.

Klasik rejimde olmayan başka bir örnekte bir beyaz cüceye çarmış olan bir yıldızın elektronlarını içeren sistemlerdir. Beyaz cücenin sıcaklığının (yüzeyde yaklaşık T=10000K) yüksek olmasına, elektron konsantrasyonun yüksek ve elektronun kütlesinin çok küçük olmasına rağmen klasik bir yakınsama öngörür ve bu durumda yine F-D istatistiklerine ihtiyaç duyulur.

Fermi-Dirac dağılımının iki çıkarımı

Kanonik dağılımdan başlayarak

Termal dengede ve içkin etkileşimleri göz ardı edilebilir N tane eş fermiyumdan oluşan bir sistem varsayın. İçkin etkileşimler göz ardı edilebildiğinden dolayı, R seviyesine sahip ait E_R enerjisine sahip çok parçacıklı sistemin enerjisi tek tek parçacıkların enerjilerinin toplamı olarak ifade edilebilir.

E_{R}=\sum _{r}n_{r}\epsilon _{r}\;

$n_{r}$ doluluk sayısı denir ve $\epsilon _{r}\;$ enerjiye sahip $r$ seviyesindeki parçacık sayısıdır. Tolam olası tüm $r$ seviyelerindeki parçacıklarının enerjilerinin eklenmesiyle bulunur.

Çok parçacıklı sistemin $R$ seviyesinde olma ihtimali düzgelenmiş kanonik dağılım ile ifade edilir.

P_{R}={\frac {e^{-\beta E_{R}}}{\displaystyle \sum _{R'}e^{-\beta E_{R'}}}}

$\beta \;$ $=1/kT$ , $k$ is Boltzmann sabiti, $T$ mutlak sıcaklık, e^{$\scriptstyle -\beta E_{R}$} Boltzmann factörü denir ve tolam olası tüm $r$ seviyelerindeki parçacıklarının enerjilerinin eklenmesiyle bulunur.. Ortalama doluluk sayısı $n_{i}\;$ değeri:

{\bar {n}}_{i}\ =\ \sum _{R}n_{i}\ P_{R}

Çok parçacıklı sistemin $R$ seviyesi tek-parçacıklı sistemin seviyelerinin parça doluluğu ile belirtilebilir, şöyle ki $n_{1},\,n_{2},\,...\;,$ belirterek, böylece

P_{R}=P_{n_{1},n_{2},...}={\frac {e^{-\beta (n_{1}\epsilon _{1}+n_{2}\epsilon _{2}+...)}}{\displaystyle \sum _{{n_{1}}',{n_{2}}',...}e^{-\beta ({n_{1}}'\epsilon _{1}+{n_{2}}'\epsilon _{2}+...)}}}

ve denklem ${\bar {n}}_{i}$ için

{\begin{alignedat}{2}{\bar {n}}_{i}&=\sum _{n_{1},n_{2},\dots }n_{i}\ P_{n_{1},n_{2},\dots }\\\\&={\frac {\displaystyle \sum _{n_{1},n_{2},\dots }n_{i}\ e^{-\beta (n_{1}\epsilon _{1}+n_{2}\epsilon _{2}+\cdots +n_{i}\epsilon _{i}+\cdots )}}{\displaystyle \sum _{n_{1},n_{2},\dots }e^{-\beta (n_{1}\epsilon _{1}+n_{2}\epsilon _{2}+\cdots +n_{i}\epsilon _{i}+\cdots )}}}\\\end{alignedat}}

Pauli dışlama prensibine göre olası tüm kombinasyonlar olan $n_{1},n_{2},...\;$ üzerinden ve her bir $r$ için $n_{r}$ = 0 or 1 üzerinden toplama yapılır. Ayrıca, her bir $n_{1},n_{2},...\;$ kambinasyonu toplam parçacık sayısının $N$ olarak tutulmasını sağlar.,

\sum _{r}n_{r}=N\;

.

Toplam serileri tekrar ayarlanırsa,

{\bar {n}}_{i}={\frac {\displaystyle \sum _{n_{i}=0}^{1}n_{i}\ e^{-\beta (n_{i}\epsilon _{i})}\quad \sideset {}{^{(i)}}\sum _{n_{1},n_{2},\dots }e^{-\beta (n_{1}\epsilon _{1}+n_{2}\epsilon _{2}+\cdots )}}{\displaystyle \sum _{n_{i}=0}^{1}e^{-\beta (n_{i}\epsilon _{i})}\qquad \sideset {}{^{(i)}}\sum _{n_{1},n_{2},\dots }e^{-\beta (n_{1}\epsilon _{1}+n_{2}\epsilon _{2}+\cdots )}}}

Toplam sembolündeki $^{(i)}$ toplamanın $n_{i}$ üzerinden olmadığını belirtir ve toplam parçacık sayısının $N_{i}=N-n_{i}$ ile değişimini belirtir. Dikkat edilmelidir ki $\Sigma ^{(i)}$ , $N_{i}$ sınırlandırması ile hala $n_{i}$ bağlıdır, çünkü $n_{i}=0$ bir durumdur ve $\Sigma ^{(i)}$ $N_{i}=N$ ile işlenir, başka bir durumda ise $n_{i}=1$ ve $\Sigma ^{(i)}$ , $N_{i}=N-1$ ile işenir;notasyonu sadeleştirmek ve $\Sigma ^{(i)}$ 'nin $N-n_{i}$ üzerinden hala $n_{i}$ dayandığını açıkça belirtmek için şunu tanımlayalım

Z_{i}(N-n_{i})\equiv \ \sideset {}{^{(i)}}\sum _{n_{1},n_{2},...}e^{-\beta (n_{1}\epsilon _{1}+n_{2}\epsilon _{2}+\cdots )}\;

${\bar {n}}_{i}$ için önceki ifade yeniden yazılabilir ve $Z_{i}$ üzerinden toplanabilir,

{\begin{alignedat}{3}{\bar {n}}_{i}\ &={\frac {\displaystyle \sum _{n_{i}=0}^{1}n_{i}\ e^{-\beta (n_{i}\epsilon _{i})}\ \ Z_{i}(N-n_{i})}{\displaystyle \sum _{n_{i}=0}^{1}e^{-\beta (n_{i}\epsilon _{i})}\qquad Z_{i}(N-n_{i})}}\\\\&=\ {\frac {\quad 0\quad \;+e^{-\beta \epsilon _{i}}\;Z_{i}(N-1)}{Z_{i}(N)+e^{-\beta \epsilon _{i}}\;Z_{i}(N-1)}}\\&=\ {\frac {1}{[Z_{i}(N)/Z_{i}(N-1)]\;e^{\beta \epsilon _{i}}+1}}\quad .\end{alignedat}}

Bir sonraki yaklaşım $Z_{i}(N)/Z_{i}(N-1)$ yerine bir ifade koymak için kullanılacaktır.

{\begin{alignedat}{2}\ln Z_{i}(N-1)&\simeq \ln Z_{i}(N)-{\frac {\partial \ln Z_{i}(N)}{\partial N}}\\&=\ln Z_{i}(N)-\alpha _{i}\;\end{alignedat}}

      $\alpha _{i}\equiv {\frac {\partial \ln Z_{i}(N)}{\partial N}}\ .$

Eğer parçacık sayısı $N$ yeterince büyük ise sisteme bir parçacık eklendiğinde kimyasal potansiyel $\mu \;$ 'deki değişim çok küçük olacaktır ve $\alpha _{i}\simeq -\mu /kT\ .$ .Her iki tarafın ters logaritmasını alıp $\alpha _{i}\,$ için yerine koyalım ve tekrar düzenleyelim

Z_{i}(N)/Z_{i}(N-1)=e^{-\mu /kT}\,

.

Yukarıdaki ifadeyi ${\bar {n}}_{i}$ için denklemde yerine koyalım ve $1/kT$ $\beta \;$ yerine koymak için $\beta \;$ önceki tanımı kullanalım .Sonuç Fermi-dirak dağılımı olacaktır.

{\bar {n}}_{i}=\ {\frac {1}{e^{(\epsilon _{i}-\mu )/kT}+1}}

Langrange çarpanları ile çıkarma

Sistemin çokluğu incelenerek ve Lagrange çarpanları incelenerek doğrudan bir sonuç elde edilebilir.

Toplam n_i tane parçacık içeren ve her biri ε_i enerji seviyelerine sahip i indeksiyle işaretlenmiş seviyeler olduğunu varsayalım. Varsayalım her biri g_i hepsi aynı enerjiye sahip ayrık ve ayrıştırılabilir alt seviyelere sahip olsun.Örneğin, iki parçacık farklı momentaya sahip olduklarında bunlar ayrıştırılabilirler, ancak aynı enerjiye sahip olabilirler.i 'ye karşılık gelen g_i değeri eşenerjilikolarak adlandırılır. Pauli dışlama ilkesi böyle her bir alt seviyeye sadece bir fermiyonun atanabileceğini belirtir.

n_i tane parçacığın g_i enerji alt seviyelerine kaç farklı yolla dağıtılabileceğini binom katsayısı ile bulunur.Binom katsayısının kombinaysonal halini kullanarak

w(n_{i},g_{i})={\frac {g_{i}!}{n_{i}!(g_{i}-n_{i})!}}\ .

Atanan n_i sayısı kümesi olan yol sayısı her bir enerji seviyesinin toplandığı değişik yolların çarğımı olarak anlaşılabilir:

W=\prod _{i}w(n_{i},g_{i})=\prod _{i}{\frac {g_{i}!}{n_{i}!(g_{i}-n_{i})!}}.

[[Maxwell-Boltzmann istatistikleri}}nin çıkarımında da aynı süreç izlenebilir.Amacımız sabit parçacık sayıyı ve sabit enerji için W 'nin enbüyük değerini verecek n_i sayıları kümesini bulmak.Sonucumuzu Lagrande çarpanlarını ile bir fonksiyon yaratarak sınırlandırıyoruz:

f(n_{i})=\ln(W)+\alpha (N-\sum n_{i})+\beta (E-\sum n_{i}\epsilon _{i}).

Faktoriyeller için Stirling yakınsamasını kullanıp n_i göre türev almak ve sonucu sıfıra eşitleyerek n_i için çözül yapılırsa Fermi-Dirac yığın sayısı elde edilir:

n_{i}={\frac {g_{i}}{e^{\alpha +\beta \epsilon _{i}}+1}}.

Termodinamik kullanılarak β = 1/kT (k Boltzmann sabiti ve Tsıcaklık veα = −μ/kT, μ kimyasal potansiyel) olduğu gösterilebilşir.Sonuç olarak bir seviyenin olasılığı:

{\bar {n}}_{i}={\frac {n_{i}}{g_{i}}}={\frac {1}{e^{(\epsilon _{i}-\mu )/kT}+1}}.

Ayrıca bakınız

Kaynakça

Reif, F. (1965). Fundamentals of Statistical and Thermal Physics. McGraw–Hill. ISBN 978-0070518001.
Blakemore, J. S. (2002). Semiconductor Statistics. Dover. ISBN 978-0486495026.
Kittel, Charles (1971). Introduction to Solid State Physics (4.4 yayıncı=John Wiley & Sons bas.). New York. ISBN 0471142867. OCLC 300039591.