Arrhenius eşitliği

Arrhenius eşitliği, fiziksel kimyada reaksiyon hızının sıcaklıkla bağıntısını gösteren bir formüldür. 1889 yılında Svante Arrhenius tarafından geliştirilmiştir. Arrhenius ise 1884 yılında denge sabitlerinin sıcaklıkla bağıntısı için Van 't Hoff eşitliğini geliştiren ve bu eşitliğin hem ileri hem de geri reaksiyonların hızları için başka bir formülün olması gerektiğine işaret ettiğini öne süren Hollandalı kimyager Jacobus Henricus van 't Hoff'un çalışmalarına dayanarak ortaya koymuştur. Bu eşitlik, kimyasal reaksiyonların hızının belirlenmesinde ve aktivasyon enerjisinin hesaplanmasında geniş ve dikkate değer bir uygulama alanına sahiptir. Arrhenius formül için fiziksel bir sağlama ve yorum ortaya koymuştur. Şu anda alanında en iyi ampirik bağıntı olarak görülmektedir. Difüzyon katsayılarının sıcaklıkla değişimini, kristal boşluklarının sayısını, sürünme oranlarını ve ısıl yollarla tetiklenen diğer birçok süreç ve reaksiyonu modellemek için kullanılabilir. 1935'te geliştirilen Eyring eşitliği de hız ve enerji arasındaki ilişkiyi ifade eder.

Formül

Neredeyse tüm uygulamalarda,$E_{a}\gg RT$ durumu geçerlidir ve k, T'nin artışıyla hızla yükselir.

Arrhenius eşitliği, bir kimyasal reaksiyonun hız sabitinin mutlak sıcaklıkla üstel bağıntısını aşağıdaki gibi tanımlar:$$k=Ae^{\frac {-E_{\text{a}}}{RT}},$$Burada:

• k hız sabitidir (bir reaksiyonda gerçekleşen çarpışmaların sıklığı),
• T mutlak sıcaklıktır,
• A frekans faktörü veya Arrhenius faktörü olarak adlandırılır. Arrhenius başlangıçta A'yı her kimyasal reaksiyon için sıcaklıktan bağımsız bir sabit olarak kabul etmiştir. Ancak daha yeni kimi uygulamalarda sıcaklıkla değişim de göz önünde bulundurulmaktadır - aşağıdaki § Modifiye edilmiş Arrhenius eşitliği'ne bakınız.
• E_a reaksiyonun molar aktivasyon enerjisidir,
• R evrensel gaz sabitidir.

  

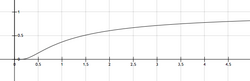
  Matematiksel olarak yüksek sıcaklıklarda $E_{a}\ll RT$ durumu geçerlidir. Bu durumda k azalır ve değeri A'ya yaklaşır (limit). Fakat bu durum pratikteki koşullarda gerçekleşmemektedir.

Eşitlik aşağıdaki gibi de ifade edilebilir:$$k=Ae^{\frac {-E_{\text{a}}}{k_{\text{B}}T}},$$Burada:

• E_a reaksiyonun aktivasyon enerjisidir (k_BT ile aynı birime sahiptir),
• k_B Boltzmann sabitidir.

Ayrıca bakınız

• Gibbs-Helmholtz denklemi

Konuyla ilgili yayınlar

• Pauling, L. C. (1988). General Chemistry. Dover Publications. 
• Laidler, K. J. (1987). Chemical Kinetics (3rd bas.). Harper & Row. 
• Laidler, K. J. (1993). The World of Physical Chemistry. Oxford University Press. 

Dış bağlantılar

• Carbon Dioxide solubility in Polyethylene - Polimerlerde kimyasal türlerin çözünürlüğünü hesaplamak için Arrhenius eşitliğinin kullanılması