Lorentz faktörü

Gama fonksiyonu ile karıştırılmamalıdır.

Lorentz faktörü veya Lorentz terimi bir cismin herhangi bir hıza sahip olmadığı durumla bir hıza sahip olması sırasında kütle, zaman ve uzay ölçümlerinde oluşacak ölçüm farklılıklarını açıklayan niceliktir. Lorentz faktörü, referans çerçeveleri arasında dönüşüm yapılabilmesini sağlayan Lorentz dönüşümünden doğar. Faktör, Lorentz elektrodinamiği içindeki erken görünümü yüzünden Hollandalı fizikçi Hendrik Lorentz adına ithaf edilmiştir.

Lorentz faktörünün aynı anda her yerde bulunması nedeniyle, genel olarak γ (Yunanca küçük gama) sembolü ile gösterilmiştir. Faktör bazen (özellikle Işıktan hızlı hareketin tartışmasında) γ yerine daha çok Γ (Yunanca büyük-gama) olarak yazılır.

Tanım

Lorentz faktörü matematiksel olarak şöyle tanımlanır:

$\gamma ={\frac {1}{\sqrt {1-v^{2}/c^{2}}}}={\frac {1}{\sqrt {1-\beta ^{2}}}}={\frac {\mathrm {d} t}{\mathrm {d} \tau }}$

burada:

• v bağıl hızdır,
• c Işığın vakumda sahip olduğu hızdır (ışık hızı).
• β v'nin c'ye bölümüdür.
• t zaman koordinatıdır.
• τ bir gözlemcinin kendi referans sisteminde gözlemlediği zaman aralığıdır. (en:Proper time)

Bu, tanımlamanın sadece bir yolu olsa da, uygulamada en çok kullanılan formudur. Tanımın alternatif formları için aşağıya bakınız.

Tanımı tamamlamak için, bazı yazarlar şöyle tanımlar:

$\alpha ={\frac {1}{\gamma }}={\sqrt {1-v^{2}/c^{2}}}\ ,$

bakınız hız ekleme formülü (Velocity-addition formula).

Lorentz faktörünün kullanımı

Aşağıda özel görelilikte Lorentz faktörünün γ olarak kullanıldığı bazı formüller gösterilmiştir:

• Lorentz dönüşümü: En basit durumda x-ekseninde referans çerçeveleri arasında düzgün doğrusal hareket (v) olduğunda bir eylemsiz referans çerçevesinden (x, y, z, t) diğer eylemsiz referans çerçevesine (x′, y′, z′, t′) göre uzayzaman koordinatlarının nasıl değiştiğini açıklar. X-ekseni dışındaki eksenler burada gösterilmemiştir.

$t'=\gamma \left(t-{\frac {vx}{c^{2}}}\right)$

$x'=\gamma \left(x-vt\right)$

Yukarıdaki dönüşümlerin sonuçları şunlardır:

• Zaman genişlemesi: Hareket eden referans çerçevesindeki birim zaman (∆t′) hareket etmeyen referans çerçevesindeki birim zamandan (∆t) daha uzundur:

$\Delta t'=\gamma \Delta t$

• Uzunluk kısalması: Bir cismin eylemsiz referans çerçevesine göre düzgün doğrusal hareket yaparken sahip olduğu birim uzunluk (∆x′) cismin eylemsiz referans çerçevesine göre hareketsiz olduğu zamanki birim uzunluğundan (∆x), kısadır. Cismin kendi durağan referans çerçevesinde de birim uzunluk ∆x olacağından hızlanan cisimlerin hız doğrultusunda kısalacağı söylenebilir.

$\Delta x'=\Delta x/\gamma$

Momentum ve enerjinin korunumu şu sonuçlara yol açar:

• Göreli kütle: Cismin eylemsiz referans çerçevesine göre düzgün doğrusal hareket yaparsa sahip olacağı kütle m cismin durgun kütlesi m₀'dan büyüktür:

$m=\gamma m_{0}$

• Göreli momentum: Göreli momentum ilişkisi klasik momentumla aynı formu alır fakat klasik kütle yeni göreli kütle kullanır:

${\vec {p}}=m{\vec {v}}=\gamma m_{0}{\vec {v}}$

• Göreli kinetik enerji: Göreli kinetik enerji cismin hareket halindeyken sahip olduğu toplam enerjiden cisim hareketsizken sahip olduğu toplam enerjinin çıkartılmasına eşittir.$E_{k}=E-E_{0}=(\gamma -1)m_{0}c^{2}$

Lorentz faktörü ($\gamma$) ${\tfrac {v}{c}}$'nin bir fonksiyonu olduğundan, göreli olmayan limit ${\textstyle \lim _{v/c\to 0}E_{k}={\tfrac {1}{2}}m_{0}v^{2}}$ olarak bulunur. Bu, kinetik enerjinin klasik mekanikteki halidir.

Sayısal değerler

Hızın bir fonksiyonu olarak Lorentz faktörünün grafiği. Lorentz faktörünün başlangıç değeri 1 (v = 0 olduğunda) olur. Hız ışık hızına yaklaştıkça (v → c) Lorentz faktörü sınırsız olarak artar (γ→ ∞).

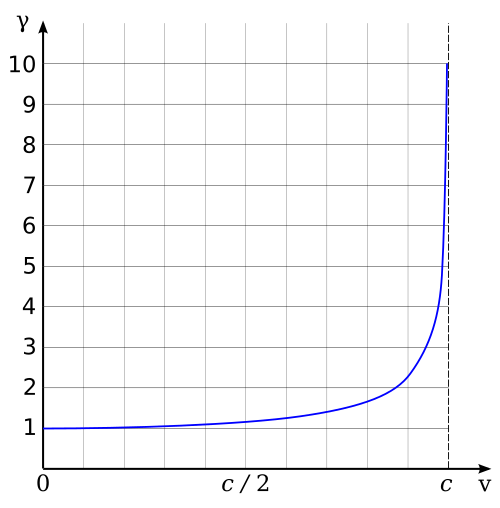
Aşağıdaki tabloda sol sütunda β, orta sütunda Lorentz faktörü, son sütunda Lorentz faktörünün tersi gösterilmiştir.

Hız (c'türünden)	Lorentz faktörü	Tersi
$\beta =v/c\,\!$	$\gamma \,\!$	$1/\gamma \,\!$
0.000	1.000	1.000
0.100	1.005	0.995
0.200	1.021	0.980
0.300	1.048	0.954
0.400	1.091	0.917
0.500	1.155	0.866
0.600	1.250	0.800
0.700	1.400	0.714
0.800	1.667	0.600
0.866	2.000	0.500
0.900	2.294	0.436
0.990	7.089	0.141
0.999	22.366	0.045

Lorentz faktörünün alternatif temsilleri

Ana maddeler: Momentum ve hız

Lorentz faktörünü yazmak için başka yollar da vardır. Yukarıda v hızı kullanıldı ama hız gibi momentum ve β de tanımlamak için uygundur.

Momentum

Göreli momentum formülünü Lorentz faktörü için çözmek şu formüle yol açar:

$\gamma ={\sqrt {1+\left({\frac {p}{m_{0}c}}\right)^{2}}}$

Bu forma çok sık rastlanılmaz fakat Maxwell-Jüttner dağılımı bu formu kullanır.

Hız oranı

Hız oranının (${\tfrac {v}{c}}$) tanımının Hiperbolik açı φ ile yapılması:

$\tanh \varphi =\beta \,\!$

Ayrıca γ (hiperbolik özdeşliklerin) kullanımı ile şuna yol açar:

$\gamma =\cosh \varphi ={\frac {1}{\sqrt {1-\tanh ^{2}\varphi }}}={\frac {1}{\sqrt {1-\beta ^{2}}}}\,\!$

Seri açılımı (hız)

Lorenz faktörünün bir Maclaurin serisi vardır:

${\begin{aligned}\gamma &={\dfrac {1}{\sqrt {1-\beta ^{2}}}}\\&=\sum _{n=0}^{\infty }\beta ^{2n}\prod _{k=1}^{n}\left({\dfrac {2k-1}{2k}}\right)\\&=1+{\frac {1}{2}}\beta ^{2}+{\frac {3}{8}}\beta ^{4}+{\frac {5}{16}}\beta ^{6}+{\frac {35}{128}}\beta ^{8}+\cdots \\\end{aligned}}$

Lorentz faktörünü γ ≈ 1 + ¹/₂ β² olarak almak düşük hızlarda göreli etkileri hesaplamak için kullanılabilir. v < 0.4 c (v < 120,000 km/s) için %1 hata payı ve v < 0.22 c (v < 66,000 km/s) için de %0.1 hata payı anlamına gelir.

Bu dizinin kısaltılmış versiyonları fizikçilerin özel göreliliğin düşük hızlarda klasik mekaniğe indirgendiğinin kanıtlamasını sağlar. Özel göreliliğin, aşağıdaki iki denklemi düşünülsün:

${\vec {p}}=\gamma m{\vec {v}}$

$E=\gamma mc^{2}\,$

γ ≈ 1 ve γ ≈ 1 + ¹/₂ β², için sırasıyla, bu onların klasik mekanikteki eşdeğerine indirger:

${\vec {p}}=m{\vec {v}}$

$E=mc^{2}+{\frac {1}{2}}mv^{2}$

Lorentz faktörü denklemi ayrıca şu şekilde tekrar yazılabilir:

$\beta ={\sqrt {1-{\frac {1}{\gamma ^{2}}}}}$

Lorentz faktörü denkleminin şu hali asimptotik bir biçime sahiptir:

$\beta =1-{\frac {1}{2}}\gamma ^{-2}-{\frac {1}{8}}\gamma ^{-4}-{\frac {1}{16}}\gamma ^{-6}-{\frac {5}{128}}\gamma ^{-8}+\cdots$

İlk iki terim zaman zaman büyük hızlı γ değerlerden hızları hesaplamak için kullanılır.

Ayrıca bakınız

• Eylemsiz referans çerçevesi
• Lorentz dönüşümü
• Yalancı hız
• Uygun hız

Dış bağlantılar

• Merrifield, Michael. "γ – Lorentz Factor (and time dilation)". Sixty Symbols. Brady Haran for the University of Nottingham. 7 Şubat 2016 tarihinde kaynağından arşivlendi. Erişim tarihi: 18 Kasım 2013. 
• Merrifield, Michael. "γ2 – Gamma Reloaded". Sixty Symbols. Brady Haran for the University of Nottingham. 7 Şubat 2016 tarihinde kaynağından arşivlendi. Erişim tarihi: 18 Kasım 2013.