Aktivasyon fonksiyonu

Yapay sinir ağındaki bir nöronun aktivasyon fonksiyonu, nöronun girdilerinden gelen değerlerin toplamını kullanarak nöronun çıktısını hesaplamaya yardımcı olan matematiksel fonksiyondur. Aktivasyon fonksiyonu doğrusal olmadığı sürece, sadece birkaç nöron kullanılarak bile karmaşık problemler çözülebilir.

Aktivasyon Fonksiyonları Tablosu

İsmi	Grafik	Fonksiyon, $g(x)$	$g$'nin türevi, $g'(x)$	Değer Kümesi	Süreklilik Sırası
Birim Fonksiyon (identity)		$x$	$1$	$(-\infty ,\infty )$	$C^{\infty }$
Heaviside basamak fonksiyonu (binary step)		${\begin{cases}0&{\text{if }}x<0\\1&{\text{if }}x\geq 0\end{cases}}$	$0$	$\{0,1\}$	$C^{-1}$
Lojistik fonksiyon (sigmoid, softstep)		$\sigma (x)\doteq {\frac {1}{1+e^{-x}}}$	$g(x)(1-g(x))$	$(0,1)$	$C^{\infty }$
Hiperbolik tanjant (tanh)		$\tanh(x)\doteq {\frac {e^{x}-e^{-x}}{e^{x}+e^{-x}}}$	$1-g(x)^{2}$	$(-1,1)$	$C^{\infty }$
Soboleva eklentili hiperbolik tanjant (smht)		$\operatorname {smht} (x)\doteq {\frac {e^{ax}-e^{-bx}}{e^{cx}+e^{-dx}}}$		$(-1,1)$	$C^{\infty }$
Doğrultulmuş Lineer birim (ReLU)		${\begin{aligned}(x)^{+}\doteq {}&{\begin{cases}0&{\text{if }}x\leq 0\\x&{\text{if }}x>0\end{cases}}\\={}&\max(0,x)=x{\textbf {1}}_{x>0}\end{aligned}}$	${\begin{cases}0&{\text{if }}x<0\\1&{\text{if }}x>0\end{cases}}$	$[0,\infty )$	$C^{0}$
Gaussian Error Lineer birim (GELU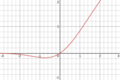)		${\begin{aligned}&{\frac {1}{2}}x\left(1+{\text{erf}}\left({\frac {x}{\sqrt {2}}}\right)\right)\\{}={}&x\Phi (x)\end{aligned}}$	$\Phi (x)+x\phi (x)$	$(-0.17\ldots ,\infty )$	$C^{\infty }$
Softplus		$\ln \left(1+e^{x}\right)$	${\frac {1}{1+e^{-x}}}$	$(0,\infty )$	$C^{\infty }$
Üstel lineer birim (ELU)		${\begin{cases}\alpha \left(e^{x}-1\right)&{\text{if }}x\leq 0\\x&{\text{if }}x>0\end{cases}}$ $\alpha$ parametresi ile	${\begin{cases}\alpha e^{x}&{\text{if }}x<0\\1&{\text{if }}x>0\end{cases}}$	$(-\alpha ,\infty )$	${\begin{cases}C^{1}&{\text{eğer }}\alpha =1{\text{ ise}}\\C^{0}&{\text{değilse}}\end{cases}}$
Ölçeklenmiş üstel lineer birim (SELU)		$\lambda {\begin{cases}\alpha (e^{x}-1)&{\text{if }}x<0\\x&{\text{if }}x\geq 0\end{cases}}$ $\lambda =1.0507$ ve $\alpha =1.67326$ parametreleri ile	$\lambda {\begin{cases}\alpha e^{x}&{\text{if }}x<0\\1&{\text{if }}x\geq 0\end{cases}}$	$(-\lambda \alpha ,\infty )$	$C^{0}$
Leaky doğrultulmuş lineer birim (Leaky ReLU)		${\begin{cases}0.01x&{\text{if }}x\leq 0\\x&{\text{if }}x>0\end{cases}}$	${\begin{cases}0.01&{\text{if }}x<0\\1&{\text{if }}x>0\end{cases}}$	$(-\infty ,\infty )$	$C^{0}$
Parametrik doğrultulmuş lineer birim (PReLU)		${\begin{cases}\alpha x&{\text{if }}x<0\\x&{\text{if }}x\geq 0\end{cases}}$ $\alpha$ parametresi ile	${\begin{cases}\alpha &{\text{if }}x<0\\1&{\text{if }}x\geq 0\end{cases}}$	$(-\infty ,\infty )$	$C^{0}$
Sigmoid lineer birim (SiLU, Sigmoid shrinkage, SiL, or Swish-1)		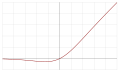${\frac {x}{1+e^{-x}}}$	${\frac {1+e^{-x}+xe^{-x}}{\left(1+e^{-x}\right)^{2}}}$	$[-0.278\ldots ,\infty )$	$C^{\infty }$
Üstel lineer sigmoid squashing (ELiSH)		${\begin{cases}{\frac {x}{1+e^{-x}}}&{\text{if }}x\geq 0\\{\frac {e^{x}-1}{1+e^{-x}}}&{\text{if }}x<0\end{cases}}$
Gauss Fonksiyonu		$e^{-x^{2}}$	$-2xe^{-x^{2}}$	$(0,1]$	$C^{\infty }$
Sinusoid		$\sin x$	$\cos x$	$[-1,1]$	$C^{\infty }$
Softmax		${\frac {e^{x_{i}}}{\sum _{j=1}^{J}e^{x_{j}}}}$ ; i = 1, …, J	$g_{i}\left({\vec {x}}\right)\left(\delta _{ij}-g_{j}\left({\vec {x}}\right)\right)$	$(0,1)$	$C^{\infty }$
Maxout		$\max _{i}x_{i}$	${\begin{cases}1&{\text{if }}j={\underset {i}{\operatorname {argmax} }}\,x_{i}\\0&{\text{if }}j\neq {\underset {i}{\operatorname {argmax} }}\,x_{i}\end{cases}}$	$(-\infty ,\infty )$	$C^{0}$

^ Yukarıdaki $\delta _{ij}$, Kronecker Deltası'dır.

^ Örneğin; $j$ önceki sinir ağı katmanının çekirdekleri (kernel) arasında yineleme yaparken, $i$ mevcut katmanın çekirdekleri arasında yineleme yapıyor olabilir.

Ayrıca Bakınız

• Yapay sinir ağları
• Lojistik fonksiyon