Vikipedi, özgür ansiklopedi
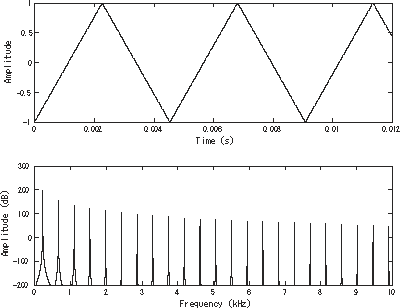
Zaman domeni (üst) ve frekans domeni (alt) grafikleri verilmiş bir üçgen dalga. Ana harmonik bileşen 220 Hz (A3)'dedir. Üçgen dalga , ismini üçgen şeklinden alan bir sinüzoidal olmayan dalga şeklidir . Üçgen dalga periyodik , parçalı lineer , sürekli gerçel bir fonksiyondur.
Aynı kare dalga gibi, üçgen dalga da sadece tek harmoniklere sahiptir. Ancak üçgen dalganın artan dereceli harmoniklerinde düşüş, kare dalgaya göre daha hızlıdır.
Artan sayıda harmoniğin toplanarak üçgen dalga elde edilmesi animasyonu. Bir üçgen dalgaya, temel frekansa tek harmonikleri eklenerek yaklaşım mümkündür. Bunun için her (4n−1). harmonik −1 ile çarpılmalı (ya da π kadar faz kaydırılmalı) ve harmonikler, harmonik derecesinin tersinin karesiyle orantılı olarak düşürülmelidir.
Elde edilen sonsuz Fourier serisi üçgen dalgaya yakınsar:
x
u
c
g
e
n
(
t
)
=
8
π
2
∑
k
=
0
∞
(
−
1
)
k
sin
(
(
2
k
+
1
)
ω
t
)
(
2
k
+
1
)
2
=
8
π
2
(
sin
(
ω
t
)
−
1
9
sin
(
3
ω
t
)
+
1
25
sin
(
5
ω
t
)
−
⋯
)
{\displaystyle {\begin{aligned}x_{\mathrm {ucgen} }(t)&{}={\frac {8}{\pi ^{2}}}\sum _{k=0}^{\infty }(-1)^{k}\,{\frac {\sin \left((2k+1)\omega t\right)}{(2k+1)^{2}}}\\&{}={\frac {8}{\pi ^{2}}}\left(\sin(\omega t)-{1 \over 9}\sin(3\omega t)+{1 \over 25}\sin(5\omega t)-\cdots \right)\end{aligned}}}
ifadede
ω
{\displaystyle \scriptstyle \omega }
açısal frekanstır . Sinüs , kare , üçgen ve testere dişi dalga şekilleriSınırları -1 ile 1 olan 2a periyotlu bir üçgen dalga şu şekilde tanımlanabilir:
x
(
t
)
=
2
a
(
t
−
a
⌊
t
a
+
1
2
⌋
)
(
−
1
)
⌊
t
a
+
1
2
⌋
{\displaystyle x(t)={\frac {2}{a}}\left(t-a\left\lfloor {\frac {t}{a}}+{\frac {1}{2}}\right\rfloor \right)(-1)^{\left\lfloor {\frac {t}{a}}+{\frac {1}{2}}\right\rfloor }}
ifadede
⌊
n
⌋
{\displaystyle \scriptstyle \lfloor n\rfloor }
n' in tam değer fonksiyonunu gösterir. Başka bir ifade şekliyle, üçgen dalga, testere dişi dalganın mutlak değeridir:
x
(
t
)
=
|
2
(
t
a
−
⌊
t
a
+
1
2
⌋
)
|
{\displaystyle x(t)=\left|2\left({t \over a}-\left\lfloor {t \over a}+{1 \over 2}\right\rfloor \right)\right|}
ya da sınırlar -1 ile 1 alınırsa:
x
(
t
)
=
2
|
2
(
t
a
−
⌊
t
a
+
1
2
⌋
)
|
−
1
{\displaystyle x(t)=2\left|2\left({t \over a}-\left\lfloor {t \over a}+{1 \over 2}\right\rfloor \right)\right|-1}
Bunların dışında üçgen dalga, kare dalganın integrali olarak da yazılabilir:
∫
sgn
(
sin
(
x
)
)
d
x
{\displaystyle \int \operatorname {sgn}(\sin(x))\,dx\,}