Display
01) Coordinate time (GM/c^3) 11) BL r coordinate (GM/c^2) 21) Radius of gyration (GM/c^2) 31) Observed framedragging rate (c^3/G/M)
02) Affine parameter (GM/c^3) 12) BL φ coordinate (radians) 22) Cartesian radius (GM/c^2) 32) Local framedragging velocity (c)
03) 1st derivative (dt/dτ) 13) BL θ coordinate (radians) 23) BH Irreducible mass (M) 33) Cartesian framedragging velocity (c)
04) Grav. time dilation (dt/dτ) 14) dr/dτ (c) 24) Kinetic energy (hf) 34) Proper velocity (c, dl/dτ)
05) Local energy (dt/dτ, mc^2) 15) dφ/dτ (c^3/G/M) 25) Potential energy (hf) 35) Observed velocity (c, d{x,y,z}/dt)
06) Cartesian radius (GM/c^2) 16) dθ/dτ (c^3/G/M) 26) Total energy (hf) 36) Escape velocity (c)
07) x Axis (GM/c^2) 17) d^2r/dτ^2 (c^6/G/M) 27) Carter constant (GMhf/c^3) 37) Local r velocity (c)
08) y Axis (GM/c^2) 18) d^2φ/dτ^2 (c^6/G^2/M^2) 28) φ angular momentum (GMhf/c^3) 38) Local θ velocity (c)
09) z Axis (GM/c^2) 19) d^2θ/dτ^2 (c^6/G^2/M^2) 29) θ angular momentum (GMhf/c^3) 39) Local φ velocity (c)
10) travelled distance (GM/c^2) 20) Spin parameter (GM^2/c) 30) Radial momentum (hf/c) 40) Total local velocity (c)
Equations of motion
All formulas come in natural units:
G
=
M
=
c
=
1
{\displaystyle {\rm {G=M=c=1}}}
Coordinate time by proper time (dt/dτ):
t
˙
=
2
E
r
(
a
2
+
r
2
)
−
2
a
L
z
r
Δ
Σ
+
E
=
ς
1
−
v
2
{\displaystyle {\rm {{\dot {t}}={\frac {2\ E\ r\ \left(a^{2}+r^{2}\right)-2\ a\ L_{z}\ r}{\Delta \ \Sigma }}+E={\frac {\varsigma }{\sqrt {1-v^{2}}}}}}}
Radial coordinate time derivative (dr/dτ):
r
˙
=
Δ
p
r
Σ
{\displaystyle {\rm {{\dot {r}}={\frac {\Delta \ p_{r}}{\Sigma }}}}}
Time derivative of the covariant momentum's r-component (pr/dτ):
p
˙
r
=
(
r
−
1
)
(
μ
(
a
2
+
r
2
)
−
k
)
+
2
E
2
r
(
a
2
+
r
2
)
−
2
a
E
L
z
+
Δ
μ
r
Δ
Σ
−
2
p
r
2
(
r
−
1
)
Σ
{\displaystyle {\rm {{\dot {p}}_{r}={\frac {(r-1)\left(\mu \ \left(a^{2}+r^{2}\right)-k\right)+2\ E^{2}\ r\left(a^{2}+r^{2}\right)-2\ a\ E\ L_{z}+\Delta \ \mu \ r}{\Delta \ \Sigma }}-{\frac {2\ p_{r}^{2}\ (r-1)}{\Sigma }}}}}
Relation to the local velocity:
p
r
=
v
r
1
+
μ
v
2
Σ
Δ
{\displaystyle {\rm {p_{r}={\frac {v_{r}}{\sqrt {1+\mu \ v^{2}}}}{\sqrt {\frac {\Sigma }{\Delta }}}}}}
Latitudinal time derivative (dθ/dτ):
θ
˙
=
p
θ
Σ
{\displaystyle {\rm {{\dot {\theta }}={\frac {p_{\theta }}{\Sigma }}}}}
Time derivative of the covariant momentum's θ-component (pθ/dτ):
p
˙
θ
=
sin
θ
cos
θ
(
L
z
2
/
sin
4
θ
−
a
2
(
E
2
+
μ
)
)
Σ
{\displaystyle {\rm {{\dot {p}}_{\theta }={\frac {\sin \theta \ \cos \theta \left(L_{z}^{2}/\sin ^{4}\theta -a^{2}\left(E^{2}+\mu \right)\right)}{\Sigma }}}}}
Relation to the local velocity:
p
θ
=
v
θ
Σ
1
+
μ
v
2
{\displaystyle {\rm {p_{\theta }={\frac {v_{\theta }\ {\sqrt {\Sigma }}}{\sqrt {1+\mu \ v^{2}}}}}}}
Longitudinal time derivative (dФ/dτ):
ϕ
˙
=
2
a
E
r
+
L
z
csc
2
θ
(
Σ
−
2
r
)
Δ
Σ
{\displaystyle {\rm {{\dot {\phi }}={\frac {2\ a\ E\ r+L_{z}\ \csc ^{2}\theta \ (\Sigma -2r)}{\Delta \ \Sigma }}}}}
Time derivative of the covariant momentum's Ф-component (pФ/dτ):
p
˙
ϕ
=
0
{\displaystyle {\rm {{\dot {p}}_{\phi }=0}}}
Carter-constant (I is the orbital inclination angel):
Q
=
p
θ
2
+
cos
2
θ
(
a
2
(
μ
2
−
E
2
)
+
L
z
2
sin
2
θ
)
=
a
2
(
μ
2
−
E
2
)
sin
2
I
+
L
z
2
tan
2
I
{\displaystyle {\rm {Q=p_{\theta }^{2}+\cos ^{2}\theta \left(a^{2}(\mu ^{2}-E^{2})+{\frac {L_{z}^{2}}{\sin ^{2}\theta }}\right)=a^{2}\ (\mu ^{2}-E^{2})\ \sin ^{2}I+L_{z}^{2}\ \tan ^{2}I}}}
Carter k (constant):
k
=
a
2
(
E
2
+
μ
)
+
L
z
2
+
Q
{\displaystyle {\rm {k=a^{2}\left(E^{2}+\mu \right)+L_{z}^{2}+Q}}}
Total energy (constant):
E
=
(
Σ
−
2
r
)
(
θ
˙
2
Δ
Σ
+
r
˙
2
Σ
−
Δ
μ
)
Δ
Σ
+
ϕ
˙
2
Δ
sin
2
θ
=
Δ
Σ
(
1
+
μ
v
2
)
χ
+
Ω
L
z
{\displaystyle {\rm {E={\sqrt {{\frac {(\Sigma -2\ r)\left({\dot {\theta }}^{2}\ \Delta \ \Sigma +{\dot {r}}^{2}\ \Sigma -\Delta \ \mu \right)}{\Delta \ \Sigma }}+{\dot {\phi }}^{2}\ \Delta \ \sin ^{2}\theta }}={\sqrt {\frac {\Delta \ \Sigma }{(1+\mu \ v^{2})\ \chi }}}+\Omega \ L_{z}}}}
Angular momentum on the Ф-axis (constant):
L
z
=
sin
2
θ
(
ϕ
˙
Δ
Σ
−
2
a
E
r
)
Σ
−
2
r
=
v
ϕ
R
¯
1
+
μ
v
2
{\displaystyle {\rm {L_{z}={\frac {\sin ^{2}\theta \ ({\dot {\phi }}\ \Delta \ \Sigma -2\ a\ E\ r)}{\Sigma -2\ r}}={\frac {v_{\phi }\ {\bar {R}}}{\sqrt {1+\mu \ v^{2}}}}}}}
with the radius of gyration
R
¯
=
χ
Σ
sin
θ
{\displaystyle {\rm {{\bar {R}}={\sqrt {\frac {\chi }{\Sigma }}}\ \sin \theta }}}
Frame Dragging angular velocity (dФ/dt):
ω
=
2
a
r
χ
{\displaystyle {\rm {\omega ={\frac {2\ a\ r}{\chi }}}}}
Gravitational time dilation (dt/dτ):
ς
=
χ
Δ
Σ
{\displaystyle {\rm {\varsigma ={\sqrt {\frac {\chi }{\Delta \ \Sigma }}}}}}
Local velocity on the r-axis:
v
r
1
+
μ
v
2
=
r
˙
Σ
Δ
{\displaystyle {\rm {{\frac {v_{r}}{\sqrt {1+\mu \ v^{2}}}}={\dot {r}}\ {\sqrt {\frac {\Sigma }{\Delta }}}}}}
Local velocity on the θ-axis:
v
θ
Σ
1
+
μ
v
2
=
θ
˙
Σ
{\displaystyle {\rm {{\frac {v_{\theta }\ {\sqrt {\Sigma }}}{\sqrt {1+\mu \ v^{2}}}}={\dot {\theta }}\ \Sigma }}}
Local velocity on the Ф-axis:
v
ϕ
1
+
μ
v
2
=
L
z
R
¯
ϕ
{\displaystyle {\frac {\rm {v_{\phi }}}{\sqrt {1+\mu \ {\rm {v^{2}}}}}}={\frac {\rm {L_{z}}}{\rm {{\bar {R}}_{\phi }}}}}
with the cartesian coordinates:
x
=
r
2
+
a
2
sin
θ
cos
ϕ
,
y
=
r
2
+
a
2
sin
θ
sin
ϕ
,
z
=
r
cos
θ
{\displaystyle {\rm {x={\sqrt {r^{2}+a^{2}}}\sin \theta \ \cos \phi \ ,\ y={\sqrt {r^{2}+a^{2}}}\sin \theta \ \sin \phi \ ,\ z=r\cos \theta \quad }}}
The observed velocity β is given by:
β
=
(
d
x
/
d
t
)
2
+
(
d
y
/
d
t
)
2
+
(
d
z
/
d
t
)
2
{\displaystyle {\rm {\beta ={\sqrt {(dx/dt)^{2}+(dy/dt)^{2}+(dz/dt)^{2}}}}}}
The local escape velocity is given by the relation:
ς
=
1
/
1
−
v
e
s
c
2
→
v
e
s
c
=
ς
2
−
1
/
ς
{\displaystyle {\rm {\varsigma =1/{\sqrt {1-v_{\rm {esc}}^{2}}}\ \to \ v_{\rm {esc}}={\sqrt {\varsigma ^{2}-1}}/\varsigma }}}
Shorthand Terms:
Σ
=
a
2
cos
2
θ
+
r
2
,
Δ
=
a
2
+
r
2
−
2
r
,
χ
=
(
a
2
+
r
2
)
2
−
a
2
sin
2
θ
Δ
{\displaystyle {\rm {\Sigma =a^{2}\cos ^{2}\theta +r^{2}\ ,\ \ \Delta =a^{2}+r^{2}-2r\ ,\ \ \chi =\left(a^{2}+r^{2}\right)^{2}-a^{2}\ \sin ^{2}\theta \ \Delta }}}
Sources: [ 1] [ 2] [ 3] [ 4] [ 5] [ 6]
References
↑ Pu, Yun, Younsi & Yoon: General-relativistic radiative transfer in Kerr spacetime , p. 2+
↑ Janna Levin & Gabe Perez-Giz: A Periodic Table for Black Hole Orbits , p. 30+
↑ Scott A. Hughes: Nearly horizon skimming orbits of Kerr black holes , p. 5+
↑ Janna Levin & Gabe Perez-Giz: The Phase Space Portrait , p. 2+
↑ Misner, Thorne & Wheeler (MTW): The Bible archive copy at the Wayback Machine
↑ Simon Tyran: Kerr Orbits / Gravitationslinsen
Lisanslama
Ben, bu işin telif sahibi, burada işi aşağıdaki lisans altında yayımlıyorum:
Şu seçeneklerde özgürsünüz:
paylaşım – eser paylaşımı, dağıtımı ve iletimiiçeriği değiştirip uyarlama – eser adaptasyonu
Aşağıdaki koşullar geçerli olacaktır:
atıf – Esere yazar veya lisans sahibi tarafından belirtilen (ancak sizi ya da eseri kullanımınızı desteklediklerini ileri sürmeyecek bir) şekilde atıfta bulunmalısınız.benzer paylaşım – Maddeyi yeniden düzenler, dönüştürür veya inşa ederseniz, katkılarınızı özgünüyle aynı veya uyumlu lisans altında dağıtmanız gerekir. https://creativecommons.org/licenses/by-sa/4.0 CC BY-SA 4.0 Creative Commons Attribution-Share Alike 4.0 true true
File usage
187
189
8
8
758
500
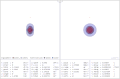
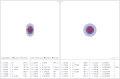
inner ergosphere and ring singularity
Türkçe Bu dosyanın temsil ettiği şeyin tek satırlık açıklamasını ekleyin.
İngilizce Photon orbit around an extremal Kerr black hole
Almanca Photonenorbit um ein maximal rotierendes schwarzes Loch